B025

Meerzone luchtstroommodellen

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Principe van een meerzone luchtstroommodel

Inzicht in de druk- en volumestroomverdeling binnen een bouwwerk kan worden verkregen met behulp van een meerzone luchtstroommodel. Hierin wordt het bouwwerk gemodelleerd tot een aantal ruimten (zones), die met elkaar en met de buitenlucht verbonden zijn via niet-lineaire luchtstroomweerstanden (zie 2.2). Deze luchtstroomweerstanden kunnen worden gevormd door roosters, kanalen, ventilatievoorzieningen, kieren, naden en dergelijke. Daarbij kunnen als randvoorwaarden temperaturen en winddrukken worden ingevoerd. Ook kan een opgelegde luchtvolumestroom worden ingevoerd (ventilator).

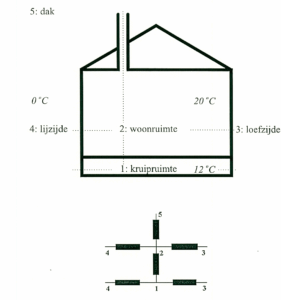
Eigenlijk kan een luchtstroommodel worden voorgesteld in een elektrisch analogon. Figuur 1 geeft een eenvoudig voorbeeld van een tweezone model, waarin de woning en de kruipruimte elk een aparte zone vormen

figuur 1. schematische doorsnede van een woning en het bijbehorende tweezone luchtstroommodel, weergegeven in een elektrisch analogon

Als bekend zijn:

de drukverdeling rond het bouwwerk;
de heersende temperaturen;
de luchtstroomweerstanden binnen het bouwwerk en in de buitenschil;
de eventuele opgelegde luchtvolumestromen (mechanische ventilatie).

Dan kan worden berekend:

de drukverdeling in het bouwwerk (in de zones);
de onbekende luchtvolumestromen (tussen de zones).

Daarnaast is het mogelijk om ook de verspreiding van verontreinigingen met een luchtstroommodel te berekenen. Daarvoor dienen additioneel bekend te zijn:

de verontreinigingsbron (grootte en plaats van de bron);
de achtergrondconcentratie in de buitenlucht (externe zones).

De fysische parameters

Winddruk- en temperatuureffecten

De grootte van de drukverschillen rond een bouwwerk, veroorzaakt door windinvloeden, hangt af van de windsnelheid en de windrichting. De drukverdeling rond een bouwwerk, en dus ook op de ventilatie-openingen van dit bouwwerk, wordt gegeven door:

(1) $\begin{equation*} \triangle P_\text{w}= \frac{1}{2} \cdot \rho \cdot C_p \cdot v^2 \end{equation*}$

Waarin:
ΔP_w= drukverschil ten gevolge van wind [Pa]
v = de windsnelheid [m/s]
C_p = plaatsafhankelijke factor (winddrukcoëfficiënt)
ρ = dichtheid van de lucht [kg/m³]

De plaatsafhankelijke factor of winddrukcoëfficiënt c_p hangt af van de oriëntatie van het vlak, het referentiepunt voor de windsnelheid v en de beschutting rond het bouwwerk. Aan de loefzijde van het bouwwerk ontstaat een overdruk, aan de overige zijden doorgaans een onderdruk.

Voor de schuine vlakken ligt de situatie gecompliceerder; vooral ter plaatse van aansluitingen aan andere vlakken is onduidelijk welke waarde voor de c_pmoet worden aangehouden. In dat geval moet een schatting gemaakt worden, bij voorbeeld door middel van interpolatie.

In bijlage 2 zijn enige praktijkwaarden voor de winddrukcoëfficiënt weergegeven in het vrije veld.

De windsnelheid hangt af van de terreinruwheid en de hoogte boven maaiveld waarop de windsnelheid van belang is. De windsnelheid wordt gegeven door:

(2) $\begin{equation*} v = v_m \cdot K \cdot z^a \end{equation*}$

Waarin:
v = plaatselijke windsnelheid [m/s]
K, a = terreincoëfficiënten (zie bijlage 3)
v_m = de windsnelheid onder meteocondities (10 m hoogte boven vrije veld) [m/s]
z = hoogte ten opzichte van maaiveld [m] (BS 5925: 1991)

De mate van beschutting rond een bouwwerk kan verdisconteerd worden in de winddrukcoëfficiënt (bijlage 2) of in de windsnelheid (bijlage 1).

De grootte van de drukverschillen, veroorzaakt door thermische trek, wordt berekend uit:

(3) $\begin{equation*} \triangle P_\text{t} = \rho_0 \cdot g \cdot h \cdot 273 \cdot \frac {(T_1 - T_2)}{(T_1 \cdot T_2)} \end{equation*}$

Waarin:
ΔP_t= thermische trek [Pa]
h = hoogteverschil (2-1) [m]
g = zwaartekrachtversnelling [m/s²]
T₁= absolute temperatuur op plaats 1 [K]
T₂= absolute temperatuur op plaats 2 [K]
ρ_o= dichtheid van lucht bij 273 K [kg/m³]

Wanneer er tussen de ventilatie-openingen van een ruimte of zone een hoogteverschil aanwezig is, speelt thermische trek een rol. Zo is het mogelijk dat zelfs bij openingen die in een gevel zijn gesitueerd (waarop in principe gelijke winddrukken heersen) luchttoevoer en luchtafvoer plaatsvindt, mits er een temperatuurverschil tussen de ruimte of zone en de buitenlucht aanwezig is (zie figuur 2).

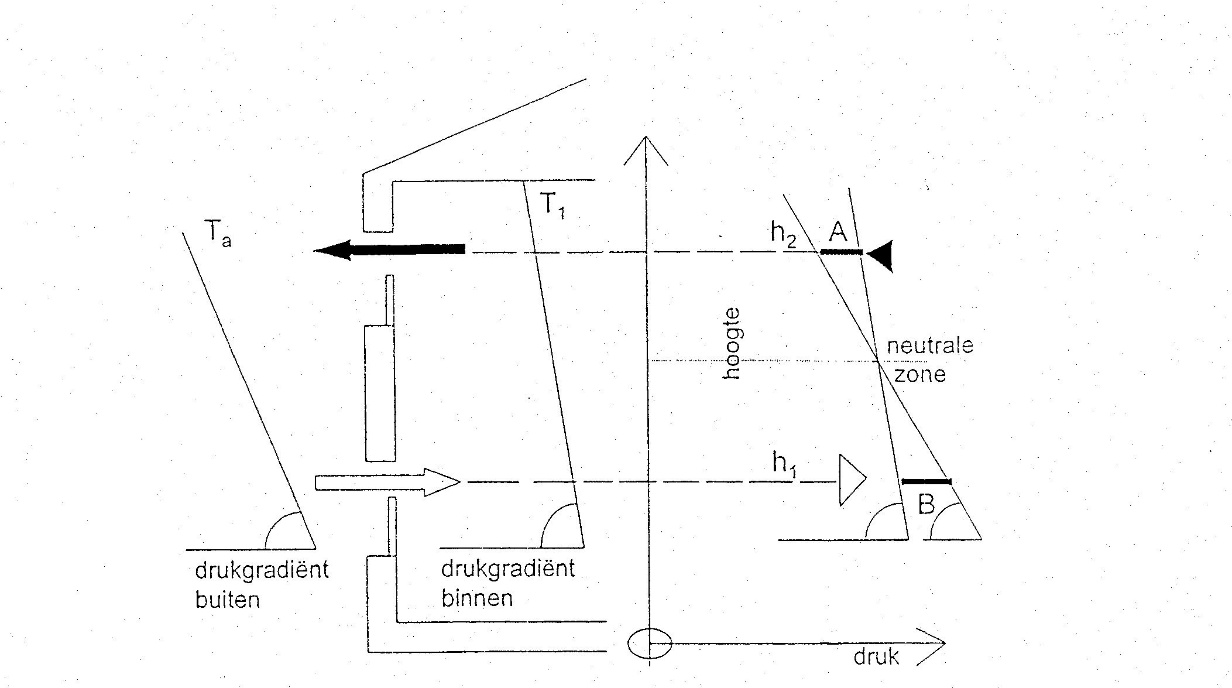
figuur 2. schematische weergave van het principe van thermische trek bij ventilatie-openingen die op verschillende hoogte in hetzelfde gevelvlak zijn gelegen

Luchtstroomweerstanden

In het model wordt een bouwwerk voorgesteld door een aantal ruimten die met elkaar en met de buitenlucht verbonden zijn via niet-lineaire luchtstroomweerstanden. Deze luchtstroomweerstanden kunnen worden gevormd door bij voorbeeld roosters, kanalen, ventilatievoorzieningen, kieren en naden. Bij een drukverschil ΔP over de luchtstroomweerstand bedraagt de luchtvolumestroom Q:

(4) $\begin{equation*} Q = C_w \cdot (\triangle P)^{\frac {1}{n} \end{equation*}$

Waarin:
$Q$ = luchtvolumestroom [m³/s]
$C_w$ = capaciteit van de luchtstroomweerstanden (luchtvolumestroom bij 1Pa drukverschil) [Paⁿm³/s]
$\triangle P$ = drukverschil [Pa]
$N$ = stromingsfactor

De stromingsfactor n varieert van 1 tot 2. Voor laminaire stroming geldt n = 1, voor turbulente stroming geldt n = 2. Wanneer n > 1 gedraagt de luchtstroomweerstand zich niet lineair.

De capaciteit van een kanaal

(5) $\begin{equation*} C = \frac{A \cdot \sqrt{\frac{2}{\rho}}}{1 + \sqrt{\frac{\lambda l}{D} + \sum \zeta_i}} \end{equation*}$

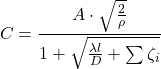
Waarbij:
A = kanaaloppervlakte in doorsnede
ρ = dichtheid van lucht
λ = wandwrijvingscoëfficiënt
l = kanaallengte
D = hydraulische diameter ( 4x oppervlakte/omtrek)
ς_i = weerstandsfactor van element i
i = het aantal weerstandverhogende elementen in het kanaal (bochten, roosters enz.)

Voor de bijbehorende stromingsfactor geldt n = 2.

De capaciteit van een opening

(6) $\begin{equation*} C = A \mu \cdot \sqrt{\frac{2}{\rho}} \end{equation*}$

Waarbij:
A = netto doorlaat van de opening [m²]
μ = contractiecoëfficiënt
ρ = dichtheid van lucht [kg/m³]

Voor de bijbehorende stromingsfactor geldt n = 2.

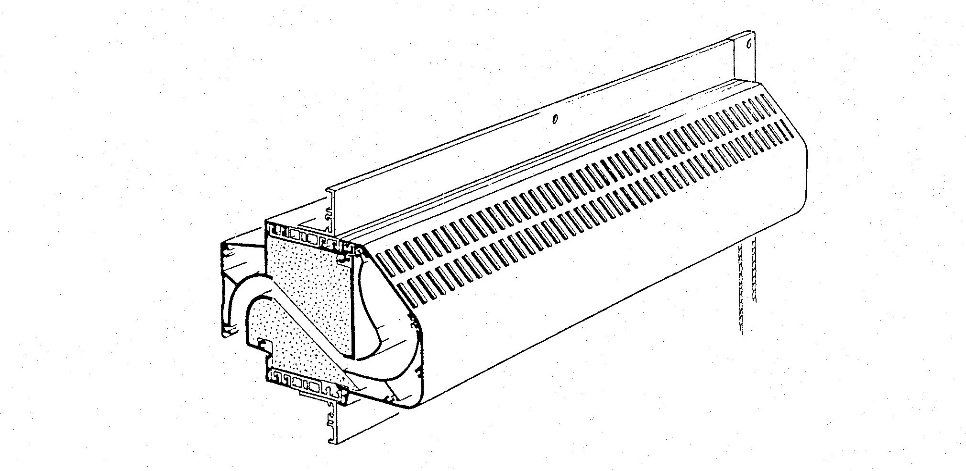
figuur 3. een geluidgedempt ventilatierooster heeft doorgaans een geringere capaciteit dan een ongedempt ventilatierooster

De capaciteit van spleten, naden en kieren

(7) $\begin{equation*} C = c \cdot l \end{equation*}$

Waarbij:
c = spleetweerstand per lengte eenheid [Paⁿm³/(s.m)]
l = totale spleetlengte [m]

Voor de bijbehorende stromingsfactor geldt 1< n < 2.
Vaak wordt gehanteerd: n=1,5.

Numerieke waarden

Voor precieze numerieke waarden van de stromingsfactor, de capaciteit, de wandenwrijvingscoëfficiënt en dergelijke kunnen diverse handboeken geraadpleegd worden. Dit geldt ook voor terreincoëfficiënten en winddrukcoëfficiënten. De bijlagen geven enkele veel gebruikte waarden.

Scalaire grootheden

Verontreinigingen

Wanneer de volumestroomverdeling binnen een bouwwerk eenmaal bekend is, kan ook de verspreiding van verontreinigingen inzichtelijk gemaakt worden. Dergelijke parameters die impliciet het gevolg zijn van het fysische model noemt men wel scalaire grootheden. Deze grootheden vormen dus geen essentieel onderdeel van het fysische model.

Bij een gegeven ventilatiedebiet en een bekende verontreinigingsbron, kan de verontreinigingsconcentratie in die zone berekend worden (stationaire beschouwing). Daarbij wordt uitgegaan van een homogene concentratieverdeling binnen de zone (homogene menging).

(8) $\begin{equation*} \triangle C_i = \frac {G}{Q_i} \end{equation*}$

Waarbij:
ΔC_i = toename verontreinigingsconcentratie in zone i [kg/m³]
G = verontreinigingsbron [kg/s]
Q_i = ventilatiedebiet (luchtvolumestroom) [m³/s]

Andere bronnen

De bronnen hoeven niet altijd verontreinigingen te introduceren in de vorm van gassen, dampen of deeltjes (zoals rook). Ook vochtbronnen introduceren een verontreiniging (waterdampconcentraties). Zelfs een warmtebron (thermisch vermogen) introduceert een verontreiniging. Bij deze bron gaat het niet om verontreinigingsconcentraties, maar om temperatuurverhoging.

Dit kan geschreven worden als:

(9) $\begin{equation*} \triangle T_i = \frac {U_\text{bron}}{ \rho c Q_i} \end{equation*}$

Waarbij:
ΔT_i = temperatuurtoename in zone i [K]
U_bron = warmtebron [W]
ρc = warmtecapaciteit [J/m³K]
Q_i = ventilatiedebiet (luchtvolumestroom) [m³/s]

Ook nu wordt weer uitgegaan van een homogene menging binnen de zone. Bovendien wordt op deze wijze geen rekening gehouden met afkoeling aan de bouwkundige scheidingsconstructies door thermische traagheid of transmissie.

Literatuur

Berekenen van de druk-volumestroomverdeling binnen een bouwwerk: VVmod versie 4.2; ir. R.A.P. van Herpen – Adviesburo Nieman BV, mei 2003
Berekening van de ventilatie in vertrekken met geopende ramen; ir. J. Huuslage – TU Delft, faculteit Civiele Techniek, mei 1991
A Guide to energy efficient ventilation; Martin W. Liddament – Air Infiltration and Ventilation Centre AIVC, GB, march 1996

Bijlage 1

terreinomschrijving	K	a
open vlak gebied	0,68	0,17
landelijk gebied met enige huizen en bomen	0,52	0,20
gebied met laagbouw ( dorpen)	0,35	0,25
gebied met hoogbouw ( stad)	0,21	0,33

tabel 1: Waarden voor de terreincoëfficiënten a en K.

Bijlage 2

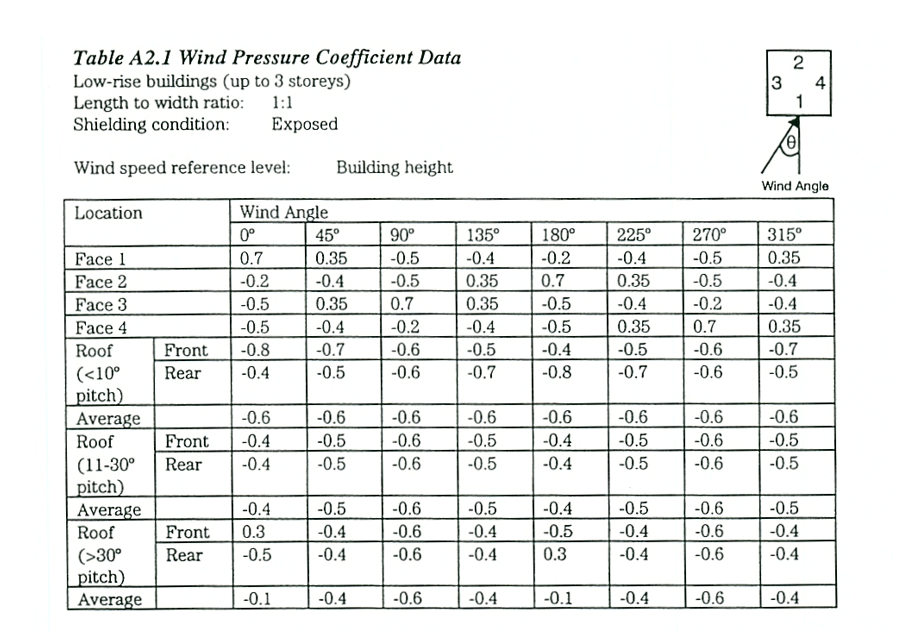
A sheet of a graph AI-generated content may be incorrect.

tabel 2: Winddrukcoëfficiënten

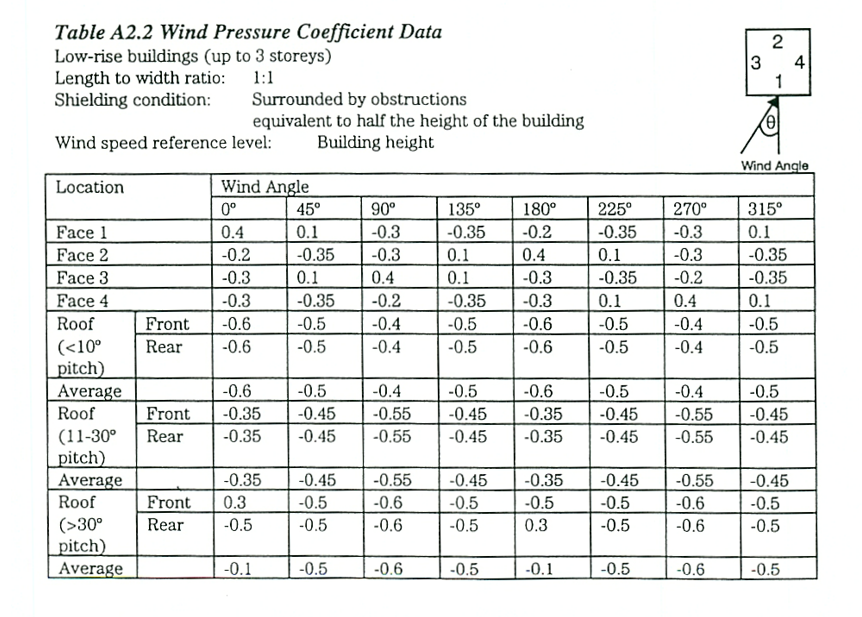
A sheet of data with numbers and lines AI-generated content may be incorrect.

tabel 3: Winddrukcoëfficiënten

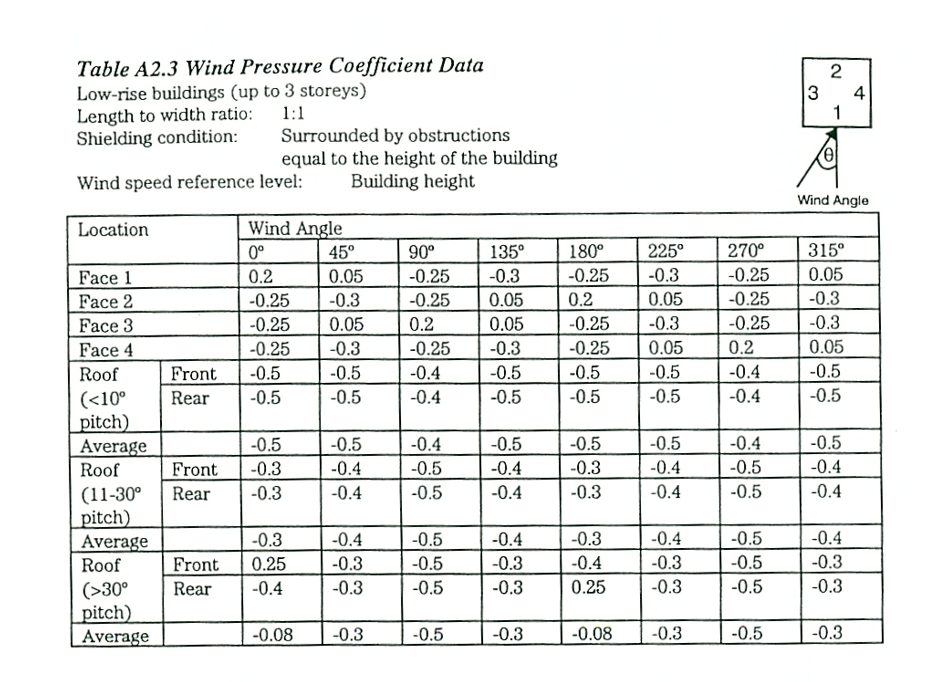
A sheet of a graph AI-generated content may be incorrect.

tabel 4: Winddrukcoëfficiënten

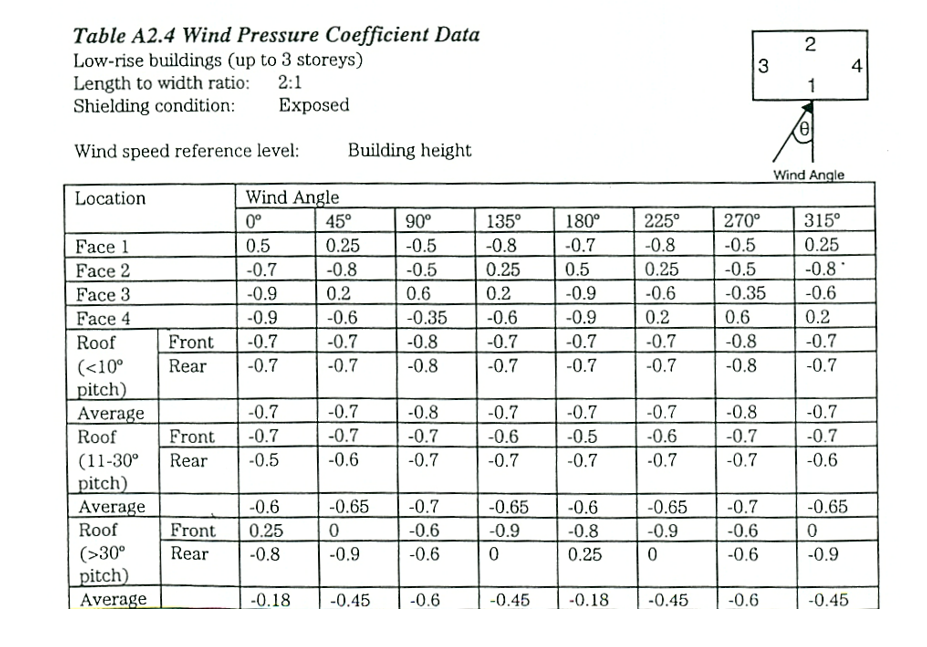
A sheet of a data sheet AI-generated content may be incorrect.

tabel 5: Winddrukcoëfficiënten

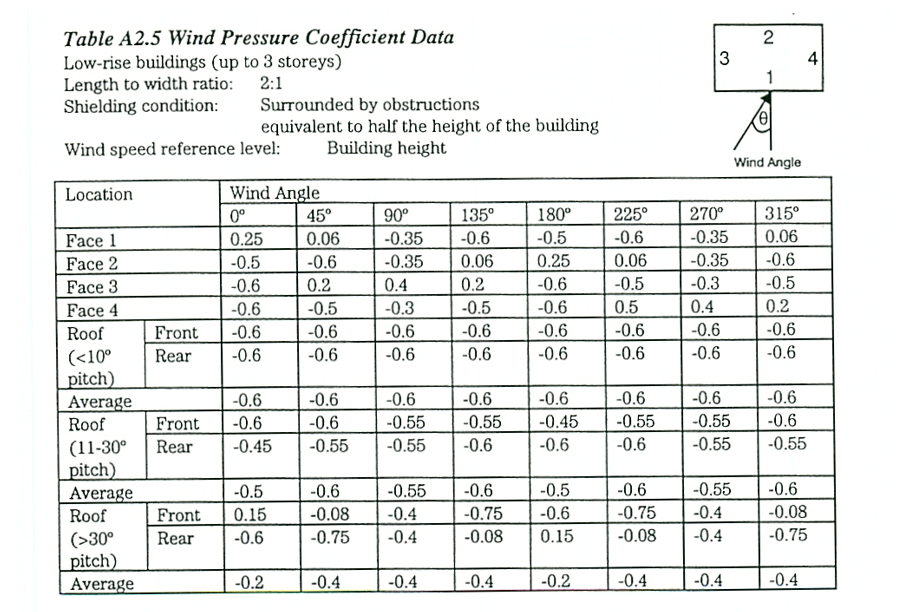
tabel 6: Winddrukcoëfficiënten

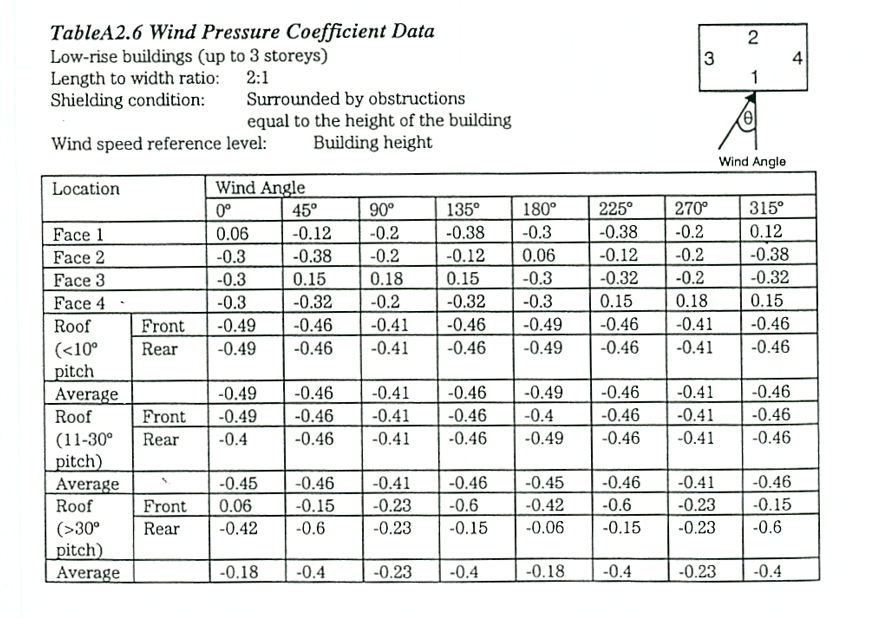
A sheet of a graph AI-generated content may be incorrect.

tabel 7: Winddrukcoëfficiënten

Bijlage 3

waarden voor de weerstandsfactor ς [-]
bocht	0,5
scherpe toevoeropening	0,5
rooster voor kanaal	1,0
kap	1,5
waarden voor de wandwrijvingscoëfficiënt λ {-]
glad kanaal (metaal, PVC)	0,035
ruw kanaal (gemetseld)	0,045
waarden voor coëfficiënt n [-]
grote openingen	2,0
spleten, kieren en naden	1,5
poreus materiaal met aansluitnaden	1,33
poreus materiaal	1,0
waarden voor weerstandcoëfficiënt C [m³/h]
grote openingen ( per cm² opening)	0,30 (n = 2)
goed sluitend raam ( per m kierlengte)	0,43 (n =1,5)
redelijke sluitend raam (per m kierlengte)	1,15 (n =1,5)
slecht sluitend raam (per m kierlengte)	3,9 (n = 1,5)
deur met tochtstrip ( per m kierlengte)	4,3 ( n = 1,5)
deur zonder tochtstrip ( per m kierlengte)	5,3 ( n = 1,5)
naden tussen kozijn / gevel ( per m kierlengte)	1,4 ( n = 1,5)
buitengevel ( per m2 geveloppervlak)	0,14 ( n = 1)

tabel 8: Enkele veel voorkomende richtwaarden voor de berekening van luchtstroomweerstanden

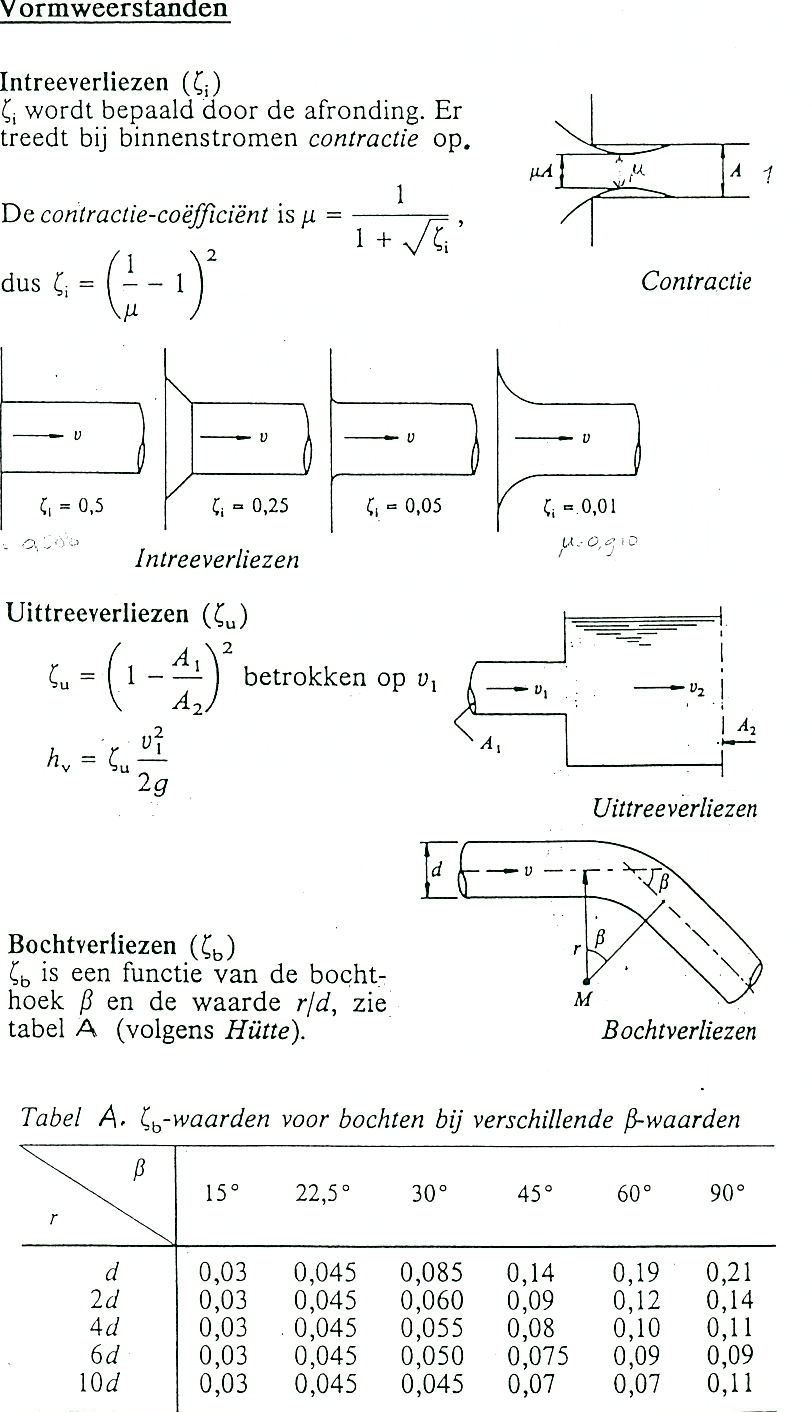
figuur 4: vormweerstanden

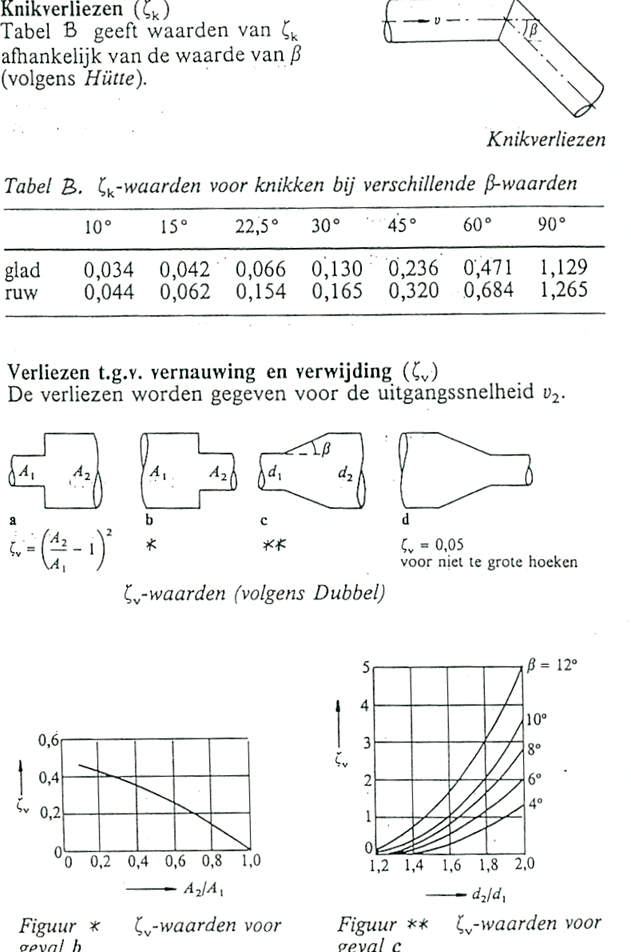
A paper with maths and graphs AI-generated content may be incorrect.

figuur 5: knikverliezen

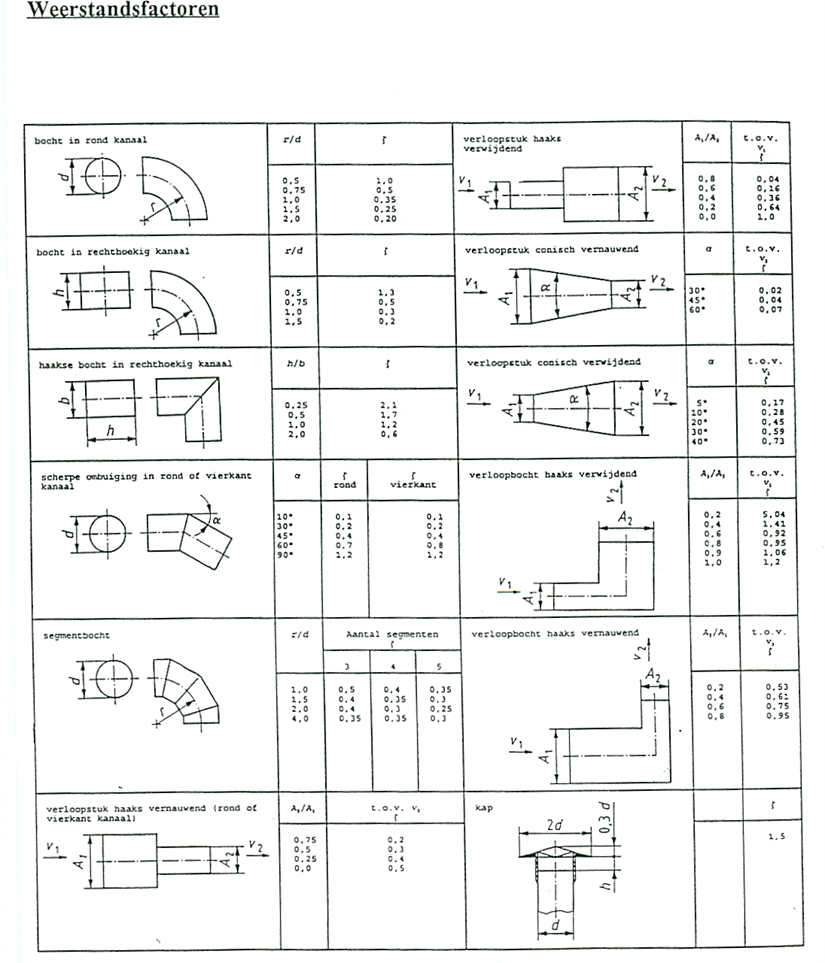
A sheet of blueprints with drawings AI-generated content may be incorrect.

figuur 6: weerstandsfactoren

Auteurs

ir. R.A.P. van Herpen

Meerzone luchtstroommodellen

Principe van een meerzone luchtstroommodel

De fysische parameters

Winddruk- en temperatuureffecten

Luchtstroomweerstanden

De capaciteit van een kanaal

De capaciteit van een opening

De capaciteit van spleten, naden en kieren

Numerieke waarden

Scalaire grootheden

Verontreinigingen

Andere bronnen

Literatuur

Bijlage 1

Bijlage 2

Bijlage 3

Auteurs

Tags

Onze partners

Over Klimapedia