A008

Nagalmtijd

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Iedereen is waarschijnlijk wel bekend met de holle, galmende klank in een leeg, ongestoffeerd en ongemeubileerd huis. De akoestiek van zo’n kale ruimte vinden we niet alleen onnatuurlijk, maar ook onaangenaam en in extreme gevallen zelfs ronduit hinderlijk, doordat we moeite hebben om anderen (en onszelf) te verstaan: reflecties worden onvoldoende gedempt door een tekort aan geluidabsorberend materiaal.

Echter, direct geluid en gereflecteerd geluid dat binnen 30 ms na elkaar arriveert, zijn voor een luisteraar niet te onderscheiden: ze “versterken” elkaar en dit positieve aspect van reflectie willen we veelal juist behouden. Bij voorbeeld omdat een spreker daardoor achter in een zaal beter verstaanbaar is; een kwestie van zuinig omspringen met akoestische energie.

Als noch een tekort noch een overmaat aan absorptie wenselijk is, dan ligt de vraag voor de hand of er wellicht een optimale hoeveelheid absorptie voor een ruimte bestaat.

Rond 1900 deed de Amerikaan Sabine hier al experimenteel onderzoek naar, wat resulteerde in een eenvoudig verband tussen het volume van een ruimte, de totale absorptie daarin en de snelheid waarmee reflecties uitdempen, uitgedrukt in de zogenaamde nagalmtijd van de ruimte.

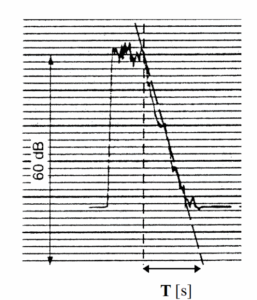
A graph of a graph AI-generated content may be incorrect.

figuur 1. nagalmtijd

De nagalmtijd wordt bepaald door in een ruimte met een geluidbron een hoog en constant geluiddrukniveau op te wekken, de bron uit te schakelen en vervolgens de tijd te meten over een afname van 60 dB in geluiddrukniveau (zie figuur 1).

In de praktijk dient men het verval over 60 dB te extrapoleren uit het eerste, lineaire gedeelte van de grafiek.

Voor diffuse ruimten kan Sabine’s relatie ook theoretisch worden afgeleid. We gaan net als bij formule (7) (zie module A007 Diffuus geluidveld) uit van formule 1 (zie module A003 Akoestisch vermogen en intensiteit), maar bedenken dat na het uitschakelen van de bron de energiedichtheid in de tijd verandert. Doordat intensiteit en energiedichtheid in een diffuus veld per definitie onafhankelijk van de plaats ondersteld mogen worden, vinden we:

(1) $\begin{equation*} 0 = \bar{I} \cdot A + V \cdot \frac{\partial E}{\partial t} \quad \text{voor} \quad t > 0 \end{equation*}$

Aangezien:

$\bar{I} = \frac{p_{\text{eff}}^2}{4 \rho c}$ (vgl. 7.14) en $E = \frac{p_{\text{eff}}^2}{\rho c^2}$ (vgl.8; module A001 Golfkarakter van geluid) schrijven we voor (1):

(2) $\begin{equation*} \bar{I} = -\frac{4V}{cA} \cdot \frac{\bar{\partial} I}{\partial t} \end{equation*}$

Met als oplossing:

(3) $\begin{equation*} \bar{I}(t) = \bar{I}(0) \cdot e^{-\frac{cAt}{4V}} \end{equation*}$

De nagalmtijd volgens Sabine volgt dan uit $10 \log \left( e^{-\frac{c A T_{\text{nagalm}}}{4V}} \right) = -60$ , met als goede benadering:

(4) $\begin{equation*} T_{\text{nagalm}} = 0,161 \cdot \frac{V}{A}\approx \frac{1}{6} \cdot \frac{V}{A} \end{equation*}$

Waarbij:
V = volume van de ruimte in m³;
A = totale absorptie in de ruimte in m² o.r.

Echter, Sabine’s formule zal ontsporen bij een ruimte, die wordt omsloten door volledig absorberende wanden: er treden geen reflecties op en er is dus ook geen nagalmtijd, in tegenstelling tot de uitkomst van formule (4) in dat geval. Deze anomalie is inherent aan het feit, dat in die situatie ook geen sprake meer is van het veronderstelde diffuse geluidveld.

Echter, voor rechthoekige ruimtes kan wel een vergelijkbare formule worden afgeleid op basis van een gemiddelde absorptiecoëfficiënt en een gemiddelde vrije weglengte tussen twee opeenvolgende reflecties zonder daarbij uit te gaan van een diffuus geluidveld.

De gemiddelde vrije weglengte bij een rechthoekig vertrek met afmetingen L_x, L_y en L_z berekenen we aan de hand van figuur 2.

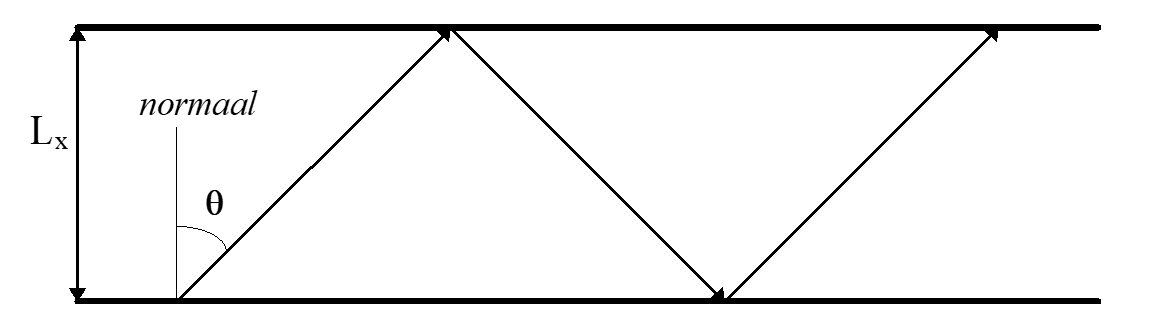
A black and white rectangular object with a white background AI-generated content may be incorrect.

figuur 2. geluidgolf die via wanden in een vertrek reflecteert

Als in figuur 2 een geluidgolf onder een hoek θ vertrekt, dan zal de afgelegde weg tot het reflectiepunt op de daaraan parallel, op afstand L_x, staande wand L_x/cosθ bedragen.

Het aantal reflecties per seconde in een willekeurige richting θ is dus:

(5) $\begin{equation*} N_x (\theta) = \frac{c}{L_x} \cos(\theta) \end{equation*}$

Dat mogelijk niet de tegenoverliggende wand wordt bereikt, maar de wand die daaraan loodrecht staat, is geen wezenlijke beperking: die wand fungeert als een spiegel en er treedt één extra reflectie op, die vanzelf meegenomen wordt in N_y of N_z.

Om het gemiddelde aantal reflecties behorend bij L_x te bepalen, dat wil zeggen de gemiddelde waarde van cosθ , gebruiken we de integratie over een halve bol, zoals bij de afleiding van formule 6 (module A007 Diffuus geluidveld) met behulp van figuur 2 (uit dezelfde module), en vinden:

(6) $\begin{equation*} \bar{N}_x = \frac{c}{L_x} \frac{1}{2\pi} \int_{\text{halve bol}} \cos(\theta) \, d\Omega = \frac{c}{2L_x} \end{equation*}$

Het gemiddelde totale aantal reflecties per seconde is dan:

(7) $\begin{equation*} \bar{N} = \bar{N}_x + \bar{N}_y + \bar{N}_z = \frac{c}{2} \left( \frac{1}{L_x} + \frac{1}{L_y} + \frac{1}{L_z} \right) = \frac{cS}{4V} \end{equation*}$

Waarbij:
S = 2(L_y·Lz+L_x·L_z+L_x·L_y) (het totaal omhullend oppervlak in m²);
V = L_x·L_y·L_z (het volume van de ruimte in m³).

Uit (7) valt voorts te concluderen, dat bij reflectie in een rechthoekige ruimte de gemiddelde vrije weglengte 4V/S bedraagt.

Elke gereflecteerde golf is gemiddeld een factor $\bar{r} = (1 - \bar{a})$ zwakker dan de invallende golf en nu kan berekend worden na hoeveel reflecties de oorspronkelijke golf 60 dB is verzwakt. De benodigde tijd daarvoor is per definitie de nagalmtijd, zodat geldt:

(8) $\begin{equation*} \bar{r}^{\bar{N}\cdot T_{\text{nagalm}}} = (1 - \bar{a})^\frac{c S T_{\text{nagalm}}}{4 V} = 10^{-6} \end{equation*}$

Daarmee vinden we de formule voor de nagalmtijd, die Eyring (1930) ontwikkelde:

(9) $\begin{equation*} T_{\text{nagalm}} = \frac{0{,}161 \cdot V}{-S \cdot \ln(1 - \bar{a})} \cong \frac{1}{6} \cdot \frac{V}{-S \cdot \ln(1 - \bar{a})} \end{equation*}$

Bij veel absorptie en voor niet-diffuse ruimten blijkt Eyring’s formule de nagalmtijd over het algemeen beter te voorspellen dan Sabine’s formule.

De nagalmtijd is een belangrijke parameter in de akoestiek van zalen en bepaalt in hoge mate de klankkwaliteit. De na te streven waarde hangt nauw samen met het gebruiksdoel van de zaal, zoals tabel 1 en figuur 9 (zie module A007 Diffuus geluidveld) aangeven; daaraan kan men als vuistregel toevoegen, dat de aanbevolen nagalmtijd toeneemt met het zaalvolume.

Meestal is de nagalmtijd voor het frequentiedomein van 500-1000 Hz maatgevend, wat samenhangt met het frequentiebereik van muziekinstrumenten en de menselijke stem.

Ruimte	Nagalmtijd
geluidstudio	0,5
klaslokaal / woonkamer	0,6 – 0,8
bioscoop	0,7 -0,9
vergaderzaal	0,7 – 1,1
theater	1,1 – 1,4
opera / kamermuziek	1,2 – 1,8
auditorium	1,5 – 1,8
concertzaal	1,7 – 2,3
kerken	1,4 – 2,6

tabel 1. aanbevolen nagalmtijd (s)

Bron	Frequentiebereik
piano	28 – 4186 Hz
viool	200 – 4000 Hz
piccolofluit	500 – 4500 Hz
hobo	250 – 1700 Hz
contrabas	30 – 200 Hz
bas	70 – 400 Hz
tenor	130 – 550 Hz
alt	200 – 800 Hz
sopraan	250 – 1100 Hz

tabel 2. frequentiebereik (Hz)

Bekend is, dat de gemeten nagalmtijd in bij voorbeeld sporthallen en grote fabrieksruimten aanzienlijk kan afwijken van de berekende nagalmtijd volgens Sabine of Eyring.

Dit wordt veroorzaakt door de ongelijkmatige verdeling van de geluidabsorptie. Vaak is deze geconcentreerd aan het plafond.

Fitzray suggereerde om de resulterende nagalmtijd voor een rechthoekige ruimte samen te stellen uit drie componenten, namelijk;

vloer-plafond reflecties;
zijwand-zijwand reflecties;
langswand-langswand reflecties.

De resulterende nagalmtijd volgens Fitzray kan berekend worden volgens:

(10) $\begin{equation*} T = \frac{0{,}161 V}{S^2} \left( \frac{2 L B}{\bar{a}_{LB}} + \frac{2 L H}{\bar{a}_{LH}} + \frac{2 B H}{\bar{a}_{BH}} \right) \end{equation*}$

Waarbij:
S = totaal wandoppervlak in m²(=2LB+2LH+2BH)
L = lengte in m
B = breedte in m
H = hoogte in m

Voor $\bar{a}_{LB} = \bar{a}_{LH} = \bar{a}_{BH} = \bar{a}$ gaat (10) over in de formule van Sabine.

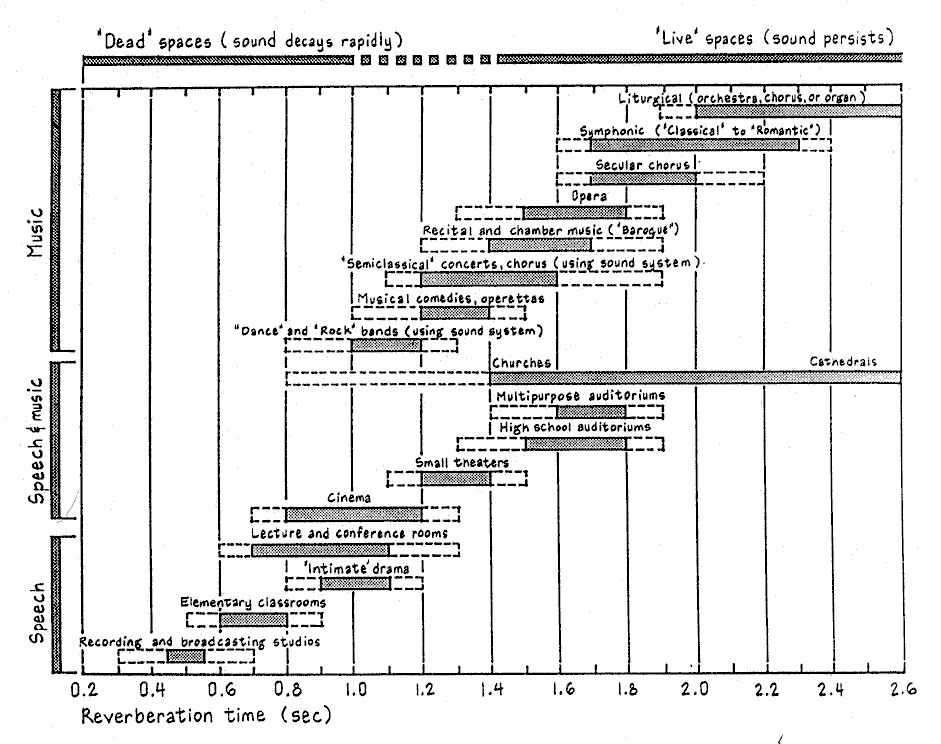
figuur 3. gewenste nagalmtijd bij spraak en muziek (bron: R.B. Newman, J.H Callender (editor), “Time-Saver Standards for Architectural Design Data”

Auteurs

ir. L. Nederlof

prof.ir. J.J.M. Cauberg

Niveau

bachelor

links

Nijsnet, Ruimteakoestiek voor architecten

Hogeschool van Amsterdam HZ University of Applied Sciences NHL Stenden Hogeschool Hanzehogeschool Groningen Hogeschool van Arnhem en Nijmegen Avans Hogeschool, Tilburg en Den Bosch De Haagse Hogeschool Hogeschool Utrecht Windesheim, Zwolle Hogeschool Inholland Alkmaar Technische Universiteit Delft Nederlands Vlaamse Bouwfysica Vereniging Stichting Kennisoverdracht Bouwfysica

Klimapedia is een kennisbank voor bouwfysica, binnenmilieu, installaties en duurzaamheid. Les- en kennismateriaal worden hier aangeboden van technische universiteiten, technische hoge scholen en vakgerichte cursussen. Docenten en cursusleiders kunnen hier hun dictaten, presentaties, toetsen, oefeningen en achtergrondinformatie delen en beschikbaar stellen voor collega’s, studenten en andere geïnteresseerden.

Nagalmtijd

Auteurs

Niveau

Tags

links

Onze partners

Over Klimapedia