A016

Luchtgeluidisolatie – Massawetten voor enkelbladige constructies

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Gebruikelijk is om geluidisolatie te beschouwen als een constructie-eigenschap, die gemeten wordt of uit metingen bekend is. Voor zover meetgegevens voorhanden én betrouwbaar zijn, doet men er ook verstandig aan om ze te gebruiken. Waar zulke gegevens ontbreken, kan men uiteraard alsnog metingen verrichten en in voorkomende gevallen zal men daartoe zelfs gedwongen worden.

Metingen zijn kostbaar en dit werpt onmiddellijk de vraag op of ze wellicht vermeden kunnen worden. Bovendien doet ontwerpen aan de hand van een alsmaar uitdijende catalogus van constructies nogal beperkt en weinig slim aan. Wat ontbreekt, is een fysisch model voor de geluidisolatie van een constructie, dat de wetmatigheden ervan onthult en een verband legt met materiaal, afmeting en opbouw. Met zo’n model hopen we dus meer inzicht te krijgen in het akoestisch gedrag van constructies om aan de hand daarvan efficiënter en gerichter te kunnen ontwerpen.

We beginnen de modelvorming door het opstellen van de bewegingsvergelijking voor een sterk vereenvoudigde situatie, te weten:

plaatvormige constructie, enkelvoudig en volkomen stijf;
oneindig uitgestrekte plaat, dat wil zeggen geen inklemming aan de randen;
loodrecht invallende, vlakke, lopende geluidgolven.

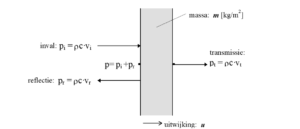
Volstaan kan dan worden met de eendimensionale beschouwing per m² in figuur 1a.

figuur 1a. Respons van een oneindig uitgestrekte starre plaat op een loodrecht invallende geluidgolf

Bij weerkaatsing van een geluidgolf tegen een vlakke constructie (zie module A015 Luchtgeluidisolatie – genormaliseerde geluidisolatie) gelden de volgende relaties in verband met:

Volkomen starre plaat:

(1) $\begin{equation*} $ v_t = \frac{\partial u}{\partial t} = v_i - v_r \rightarrow p_t = p_i - p_r $ \end{equation*}$

Resulterende druk links:

(2) $\begin{equation*} p = p_i + p_r\rightarrow p+p_t = 2p_i \end{equation*}$

Beweging van de plaat:

(3) $\begin{equation*} p - p_t = m \frac{\partial^2 u}{\partial^2 t} \rightarrow p - p_t = m\frac{\partial V_t}{\partial t} \end{equation*}$

Via eliminatie van p komen we tot de volgende differentiaalvergelijking:

(4) $\begin{equation*} p_i = p_t + \frac{m}{2 \rho c} \frac{\partial p_t}{\partial t} \end{equation*}$

De algemene oplossing van dit type differentiaalvergelijking is zodanig, dat als p_i sinusvormig is, ook p_t sinusvormig is en omgekeerd. Immers, door in voorgaande vergelijking te stellen, $p_t = \hat{p}_t \sin(2 \pi f \cdot t)$ volgt :

(5) $\begin{equation*} \begin{aligned} p_i = \hat{p}_t \sin(2 \pi f t) + \frac{2 \pi f m}{2 \rho c} \hat{p}_t \cos(2 \pi f t) = \\ = \hat{p} \sqrt{1 + \left(\frac{\pi f m}{p c}\right)^2} \cdot \sin\left( 2 \pi f t + \arctg \ arctg\left( \frac{\pi f m}{p c} \right) \right) \] \end{aligned} \end{equation*}$

Hieruit zien we dat p_i inderdaad sinusvormig is, waarbij voor de amplitudes geldt:

(6) $\begin{equation*} \frac{\hat{p}_i^2}{\hat{p}_t^2} = 1 + \left(\frac{\pi f m}{\rho c}\right)^2 \text{voor loodrechte inval} \end{equation*}$

Een geluidintensiteit is evenredig met het kwadraat van de effectieve geluiddruk, dus ook met het kwadraat van diens amplitude. Volgens de definitie van de geluidisolatie hebben we daarmee een relatie gevonden, die bekend staat als de theoretische massawet voor enkelvoudige constructies bij loodrechte inval:

(7) $\begin{equation*} R_\perp = 10 \log \left[ 1 + \left( \frac{\pi f m}{\rho c} \right)^2 \right] \approx 20 \log(m) + 20 \log\left(\frac{f}{500}\right) + 12 \] \end{equation*}$

Waarin:
R_⊥ = theoretische geluidisolatie bij loodrechte inval [dB]
M = massa per vierkante meter constructie [kg/m²]
f = (midden)frequentie [Hz]

De benadering in het rechterdeel van (7) geldt zolang fm>>ρc/π ≈130. Aangezien we meestal octaven van 63Hz en hoger beschouwen, komt deze eis neer op m>>2 kg/m².

Schuin invallend geluid kan op vergelijkbare wijze behandeld worden door in formule 1 t/m 3 eenvoudig de componenten van v_i, v_r en v_t langs de normaal op de constructie te nemen; dat wil zeggen met cosθ te vermenigvuldigen (zie figuur 1b).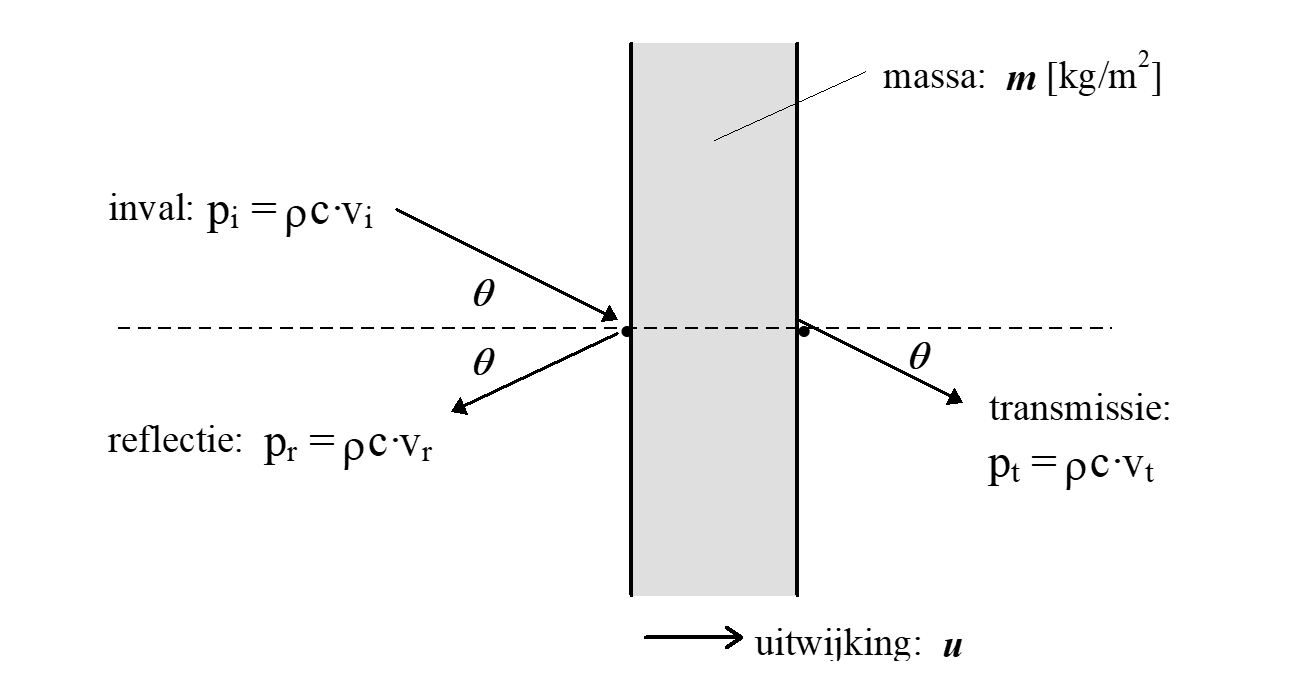

figuur 1b. repons van een oneindig uitgestrekte starre plaat op een schuin invallende geluidgolf

Het kost weinig moeite om in te zien dat formule (6) dan overgaat in:

(8) $\begin{equation*} \frac{\hat{p}_i^2}{\hat{p}_t^2} = 1 + \left( \frac{\pi f m \cdot \cos \theta}{\rho c} \right) \text{voor schuine inval} \end{equation*}$

Omdat cosθ ≤1 kan hieruit geconcludeerd worden, dat de geluidisolatie voor schuin invallend geluid slechter zal zijn dan voor loodrecht invallend geluid. Echter, in de praktijk heeft men te maken met alzijdig invallend geluid, zodat het zinvol is om een gemiddelde waarde van cos²θ te bepalen voor alle invalsrichtingen. Daarvoor nemen we weer een halve eenheidsbol rond het punt van inval en gebruiken de rotatiesymmetrie om de normaal om een ruimtehoekje dΩ te benaderen door dΩ=2π.sinθ .dθ , waarbij θ varieert tussen 0 en π/2; zodat

(9) $\begin{equation*} \frac{1}{2\pi} \int\limits_{\text{halve bol}} \cos^2 \theta \, d\Omega = \frac{1}{2\pi} \int\limits_0^{\pi/2} 2\pi \sin \theta \cos^2 \theta \, d\theta = \frac{1}{3} \end{equation*}$

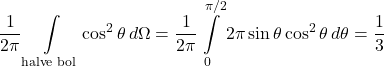
De theoretische massawet voor alzijdige inval ligt dus 10·log(3) ≈5 dB lager dan die voor loodrechte inval volgens formule (7). Het voorgaande model voorspelt een toename van de geluidisolatie bij grotere massa en hogere frequentie en wel met 6 dB per verdubbeling. In de praktijk blijkt die stijging circa 5 dB per verdubbeling te bedragen, verloopt de isolatiecurve meestal minder recht én liggen de waarden ook wat lager dan voorspeld. Meetresultaten hebben dan ook geleid tot formulering van een aangepaste massawet, de praktische massawet voor enkelvoudige constructies bij alzijdige inval, welke (inderdaad) stijgt met 17,5.log(2) ≈5 dB/octaaf:

(10) $\begin{equation*} R_p = 17,5 \log(m) + 17,5 \log\left(\frac{f}{500}\right) + 3 \; [\mathrm{dB}] \end{equation*}$

Omdat de praktische massawet is afgeleid uit de gemeten isolatiecurve van een groot aantal verschillende constructies geeft formule (10) slechts een gemiddeld verloop weer. Afwijkingen zijn daaruit weggemiddeld vanuit een hypothese omtrent de geldigheid en volledigheid van de theoretische massawet. Voor de meetfouten is dat terecht, maar sommige anomaliën wijzen toch op een tekortkoming in dit massawetmodel. Ter illustratie daarvan is in figuur 2 de isolatiecurve van enkele constructies uitgezet volgens de praktische massawet en de theoretische massawet (bij alzijdige inval), met ter vergelijking de (meet)waarden die het “Besluit geluidwering gebouwen”(Bgg) als karakteristiek hanteert. Daaruit blijkt, dat het succes van de massawetten in het voorspellen van de geluidisolatie nogal wisselend is, eufemistisch gezegd.

Helemaal onverwacht is het verschil tussen theorie en praktijk niet, want totaal genegeerd is tot nu toe het gedrag van de plaat in langsrichting. Bovendien is aangetoond, dat transmissie onder grotere invalshoeken volgens een “stralendoorgangs-model eigenlijk onmogelijk is. En dat is juist wat bij figuur 1 stilzwijgend is verondersteld: de “ wet van Snellius” is toegepast op beide grensvlakken van de constructie en daardoor maken v_i en v_t dezelfde hoek θ met de normaal.

Een beter model kan daarom alleen verkregen worden door ook buiggolven daarin te betrekken. Dit wordt coïncidentie genoemd.

paneelopbouw:

2×9,5 mm gipskarton

30 mm polyurethaan

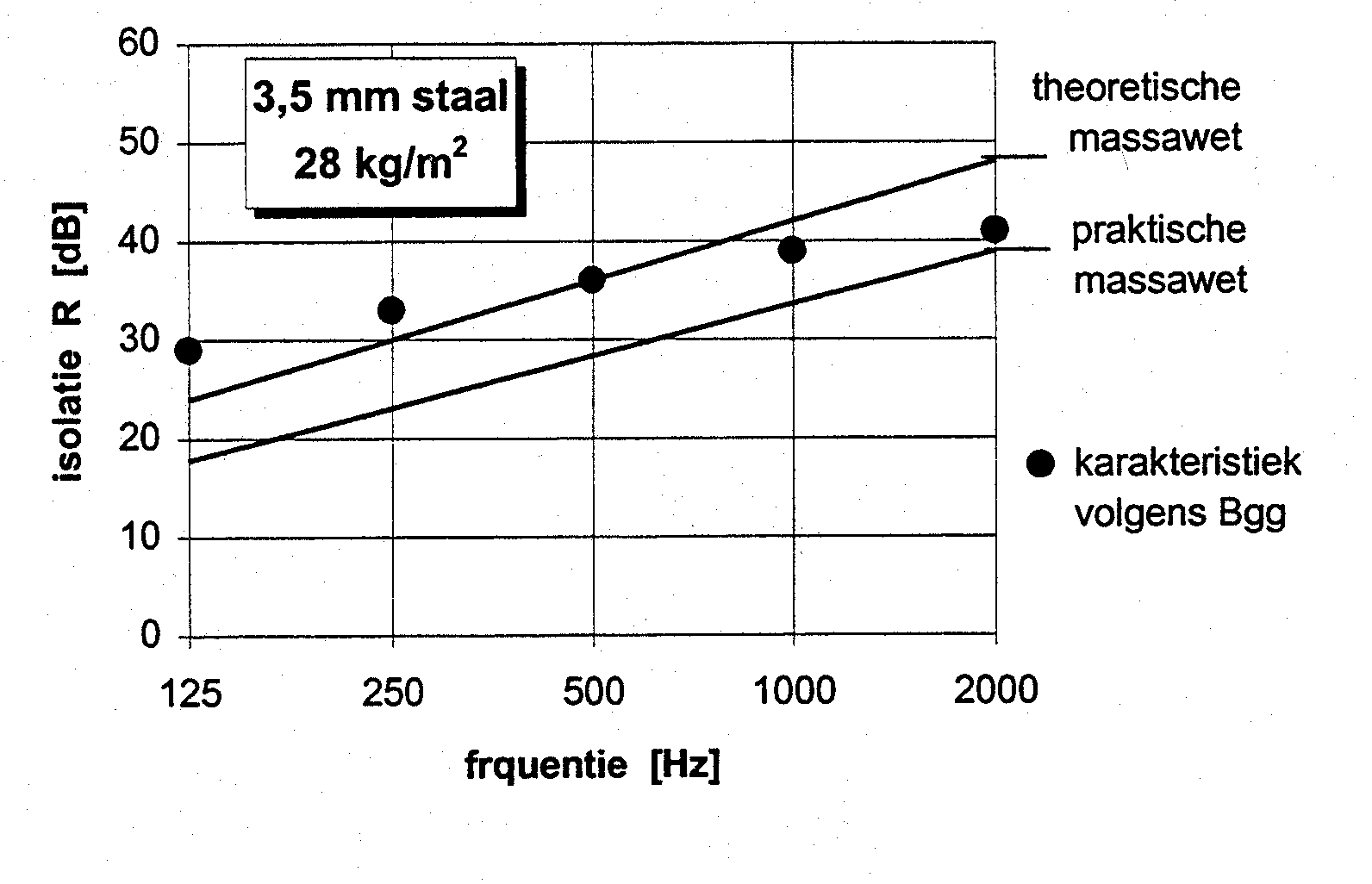
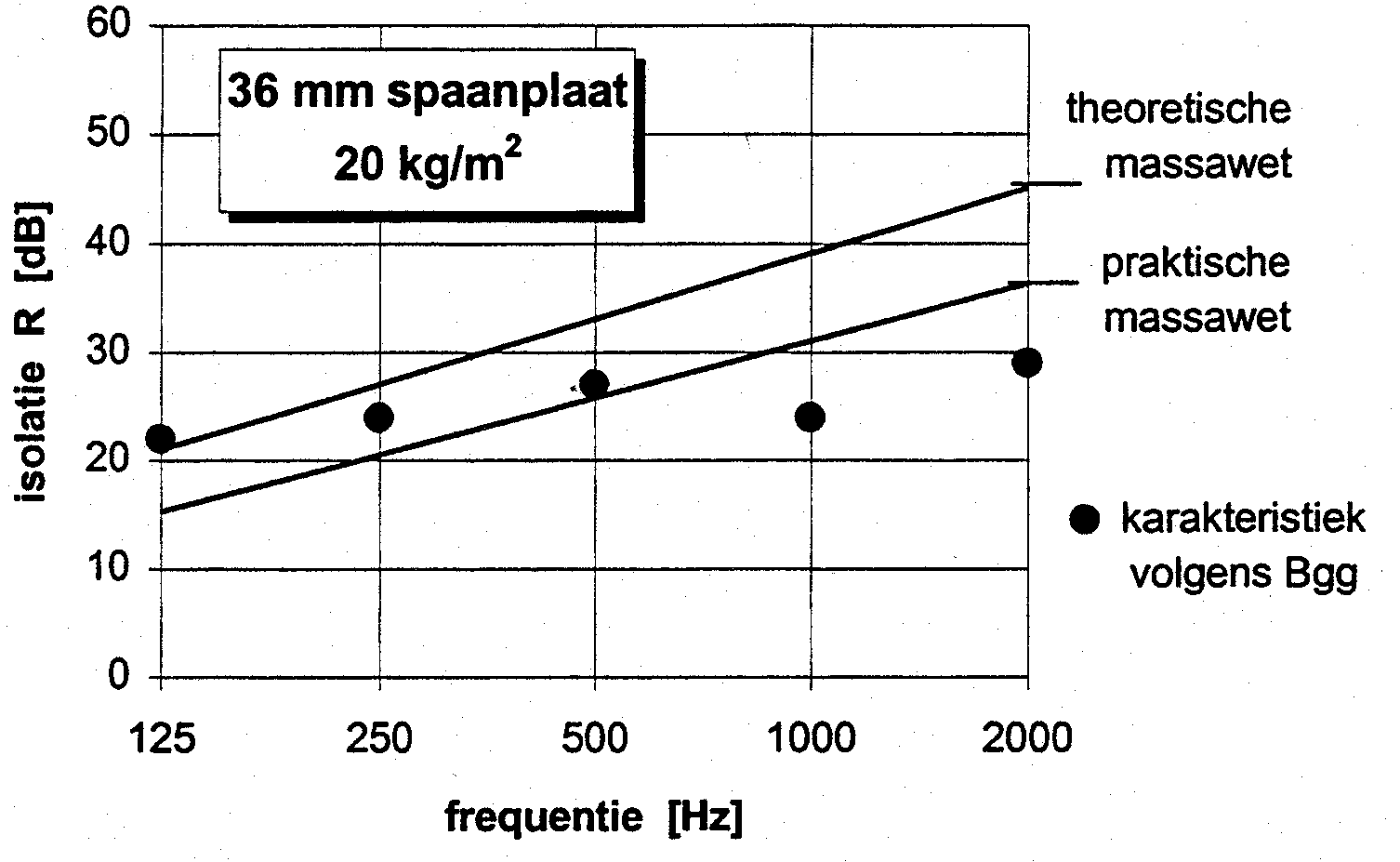
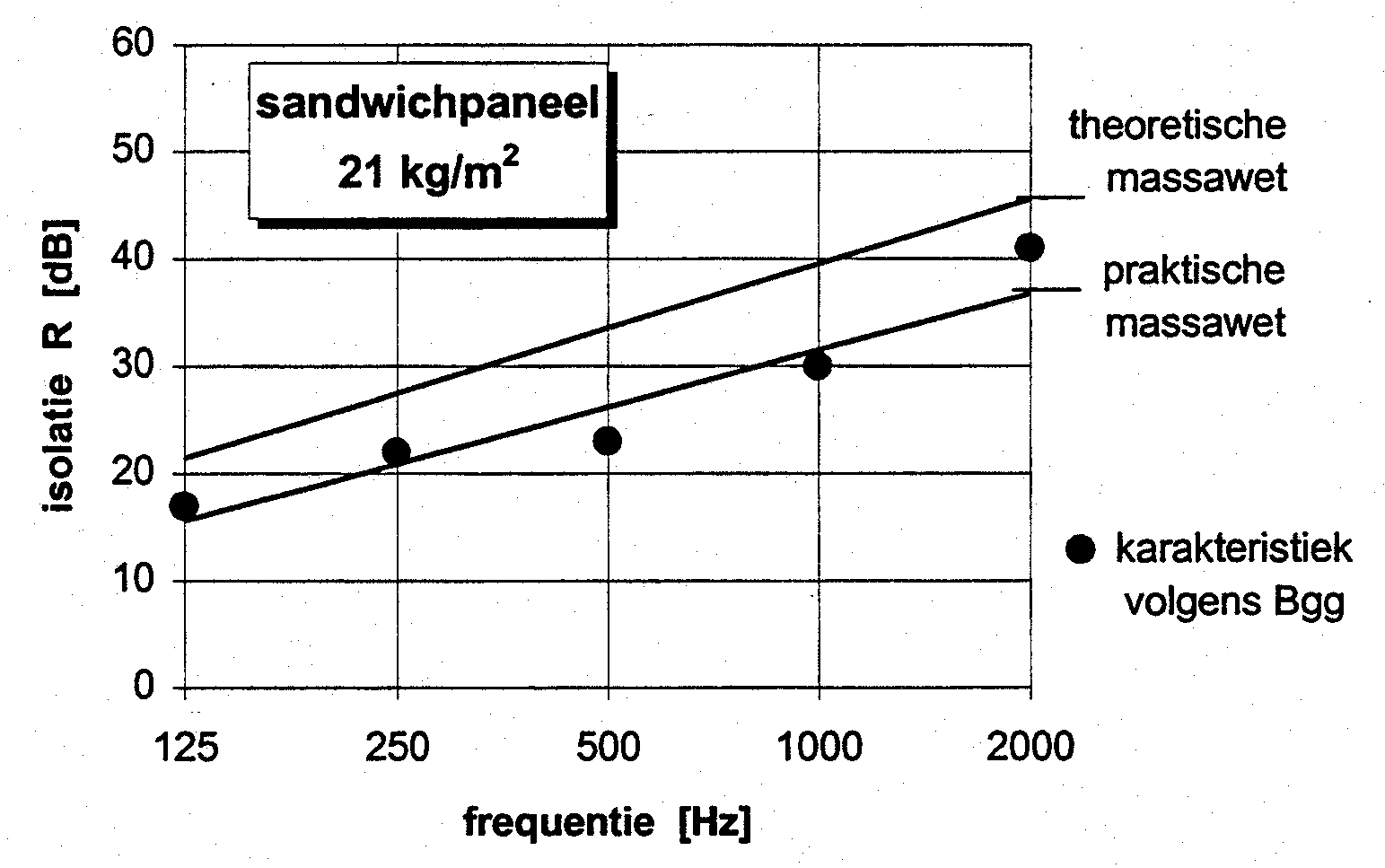
figuur 2. vergelijking massawetten met de karakteristieke praktijkwaarden

Auteurs

ir. L. Nederlof

prof.ir. J.J.M. Cauberg

Niveau

bachelor

master

Luchtgeluidisolatie – Massawetten voor enkelbladige constructies

Auteurs

Niveau

Tags

Onze partners

Over Klimapedia