KLIMAPEDIA

A015

Genormaliseerde luchtgeluidisolatie

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Geluid dat in een vertrek wordt geproduceerd, brengt via de lucht ook de omhullende constructie in trilling. Dientengevolge zal het geluid langs verschillende wegen doordringen in een naastliggende ruimte, waardoor een hinderlijk geluidniveau kan worden veroorzaakt. De mogelijke transmissiewegen zijn schematisch weergegeven in figuur 1. Daarbij wordt onderscheid gemaakt tussen directe transmissie via de scheidingsconstructie en zogenaamde flankerende transmissie, waar alle overige (indirecte) transmissiewegen in worden vervat, voor zover deze berusten op trillingoverdracht in de omhullende constructie.

A diagram of a circuit AI-generated content may be incorrect.

figuur 1. Directe (1) en flankerende transmissie (2+3+4)

Naast directe en flankerende transmissie kan er ook nog sprake zijn van geluidlekken rond de scheidingsconstructie en van geluidoverdracht via aanpalende ruimten, het zogenaamde omloopgeluid.

Voor de geluidisolatie tussen de vertrekken in figuur 1 is in eerste instantie de transmissie door de scheidingsconstructie maatgevend. Daarom zal het begrip luchtgeluidisolatie eerst worden uitgedrukt in een meer handzame vorm, gebaseerd op de (meetbare) geluiddrukniveaus in het zend- en ontvangvertrek. Vooralsnog behandelen we dus alleen de directe transmissie en daarbij gaan we ervan uit, dat het geluidveld aan weerszijden van de scheidingsconstructie bij benadering diffuus is.

De invallende geluidintensiteit op de scheidingsconstructie aan de zendkant bedraagt:

(1) $\begin{equation*} I_{\text{zend}} = \frac{p_{\text{eff,zend}}^2}{4 \rho c} \end{equation*}$

hetgeen over een oppervlak S met transmissiecoëfficiënt t aan de ontvangkant een akoestisch vermogen de ruimte binnenbrengt ter grootte van:

(2) $\begin{equation*} W_{\text{ontv}} = S \cdot T \cdot I_{\text{zend}} \end{equation*}$

Dit veroorzaakt in het ontvangvertrek een (gemiddelde) intensiteit, waarvoor geldt:

(3) $\begin{equation*} I_{\text{ontv}} = \frac{p_{\text{eff,ontv}}^2}{4 \rho c} = \frac{W_{\text{ontv}}}{A_{\text{ontv}}} = \frac{S}{A_{\text{ontv}}} \cdot t \cdot \frac{p_{\text{eff,zend}}^2}{4 \rho c} \end{equation*}$

Waaruit volgt:

(4) $\begin{equation*} \frac{1}{t} = \frac{p_{\text{eff,zend}}^2}{p_0^2} \cdot \frac{p_0^2}{p_{\text{eff,ontv}}^2} \cdot \frac{S}{A_{\text{ontv}}} \end{equation*}$

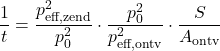
Hieruit volgt de definitie van de genormaliseerde luchtgeluidisolatie:

(5) $\begin{equation*} R_{\text{lu}} = L_{\text{zend}} - L_{\text{ontv}} + 10 \log \frac{S}{A_{\text{ontv}}} \ [\text{dB}] \end{equation*}$

Waarin:
L_zend = geluiddrukniveau in het zendvertrek [dB]
L_{ontv =}geluiddrukniveau in het ontvangvertrek [dB]
S = oppervlak van de scheidingsconstructie [m²]
A_ontv = totale absorptie in het ontvangvertrek [m² o.r.]

Formule (5) is uiterst bedrieglijk, omdat R_lu ogenschijnlijk afhangt van S en A_ontv. Echter, het tegendeel is waar: elke variatie in S of A_ontv veroorzaakt een verandering in L_ontv, zodanig dat de term $L_{\text{ontv}} - 10 \log \frac{S}{A_{\text{ontv}}}$ gelijk blijft en dus ook R_lu!

Met andere woorden: het geluidniveau in het ontvangvertrek is genormaliseerd. Met behulp van (5) kan de luchtgeluidisolatie van een constructie aan de hand van metingen bepaald worden, mits flankerend transmissie, omloopgeluid en geluidlekken geen rol spelen. Zulke ideale omstandigheden zijn vrijwel uitsluitend in een specifiek geluidtechnisch laboratorium te realiseren. Zoals we later bij de massawetten zullen zien, kan de luchtgeluidisolatie voor eenvoudige (monolitische) constructies nog wel berekend worden uit het gewicht per m², maar bij meer complexe elementen als spouwconstructies, ventilatieroosters en suskasten zal vaak slechts een laboratoriummeting hiervoor uitkomst kunnen bieden. Voor een aantal veel gebruikte constructies zijn de resultaten van dergelijke metingen en berekeningen vermeld in publicaties van het Ministerie van VROM .

Is de luchtgeluidisolatie van een constructie eenmaal bekend, dan levert een iets andere schrijfwijze van (5) een praktisch instrument voor de prognose van het ontvangen geluiddrukniveau ten gevolge van directe transmissie tussen diffuse ruimten:

(6) $\begin{equation*} L_{\text{ontv}} = L_{\text{zend}} - R_{\text{lu}} + 10 \log \frac{S}{A_{\text{ontv}}} \ [\text{dB}] \end{equation*}$

In de praktijk blijkt – bij een goed uitgevoerde constructie – het aldus voorspelde geluid-drukniveau 1 à 2 dB hoger te liggen ten gevolge van flankerende transmissie en geluidlekken via naden bij de randaansluitingen.

	geluidisolatie enkelvoudige muren in dB bij					R_A
massa [kg/m²]	125 Hz	250 Hz	500 Hz	1 kHz	2 kHz	dB(A)
80 – 100	33	35	36	41	48	38
101 – 125	34	35	37	43	50	39
126 – 160	34	36	39	45	51	41
161 – 200	35	38	42	48	53	43
201 – 250	36	39	44	50	55	44
251 – 320	38	42	46	52	57	47
321 – 400	40	44	49	54	59	49
401 – 500	42	45	50	55	60	50
501 – 630	44	47	52	57	61	52
631 – 800	45	48	53	58	62	53

tabel 1a. isolatiewaarden enkelvoudige steenachtige muren

	geluidisolatie spouwmuren in dB bij					R_A
massa [kg/m²]	125 Hz	250 Hz	500 Hz	1 kHz	2 kHz	dB(A)
161 – 200	37	42	45	52	59	46
201 – 250	38	42	48	55	61	48
251 – 320	39	43	50	57	63	49
321 – 400	40	43	50	58	64	49
401 – 500	42	46	52	59	65	52

tabel 1b. isolatiewaarden steenachtige spouwmuren

	geluidisolatie dubbel glas in dB bij					R_A
opbouw [mm]	125 Hz	250 Hz	500 Hz	1 kHz	2 kHz	dB(A)
4- 6- 4	22	23	23	32	35	26
4-12- 4	22	22	28	36	38	29
4-12- 6	22	21	29	37	37	29
4-12- 8	23	21	30	36	36	29
4-12-10	24	20	30	34	34	28
6-12- 6	23	20	31	36	31	28
6-12- 8	23	21	31	35	30	28
6-12-10	24	23	32	33	33	30
6-12-12	24	23	32	33	33	30
8-12- 8	24	23	32	35	31	30
8-12-10	24	25	33	33	32	31
8-12-12	24	26	33	33	33	31
4-25- 4	21	24	32	40	42	30
4-25- 6	22	26	33	41	41	32
4-25- 8	22	27	34	40	40	32
4-25-10	23	27	34	38	38	32
6-25- 6	22	27	35	40	35	32
6-25- 8	23	24	35	39	34	31
6-25-10	23	28	36	38	38	33
8-25- 8	22	29	36	39	35	33
8-25-10	22	29	37	37	36	32

tabel 1c. isolatiewaarden dubbel glas bij spouwbreedte 6-25 mm

	geluidisolatie dubbel glas in dB bij					R_A
opbouw [mm]	125 Hz	250 Hz	500 Hz	1 kHz	2 kHz	dB(A)
4- 50- 4	21	29	36	44	46	33
4- 50- 6	21	30	37	45	45	33
4- 50- 8	20	30	38	43	43	33
4- 50-10	20	31	38	42	42	32
6- 50- 6	20	31	38	44	39	33
6- 50- 8	22	32	39	43	38	34
6- 50-10	23	32	40	42	42	35
8- 50- 8	24	32	40	42	39	36
8- 50-10	25	33	40	40	40	36
8- 50-12	26	33	41	41	41	37
4-100- 4	24	32	40	48	50	38
4-100- 6	26	33	41	49	49	38
4-100- 8	27	34	42	47	47	38
4-100-10	27	34	42	46	46	38
6-100- 6	27	35	42	48	43	39
6-100- 8	28	35	43	47	42	39
6-100-10	28	36	43	46	46	40
6-100-12	29	36	44	45	45	40
8-100- 8	29	36	44	46	43	40
8-100-10	29	37	44	44	43	40
8-100-12	30	37	45	45	45	41

tabel 1d. isolatiewaarden dubbel glas bij spouwbreedte 50-100 mm

	geluidisolatie gas gevuld & gelamineerd in dB bij:					R_A
opbouw [mm] [kg/m²]	125 Hz	250 Hz	500 Hz	1 kHz	2 kHz	dB(A)
6- 12- 9	25	26	40	51	48	34
12- 12- 9	27	30	38	39	43	36
6- 20- 9	24	33	44	50	48	36
7- 12- 9	26	27	42	47	44	35
7- 20- 9	24	35	43	50	46	37
9- 20-11	25	40	51	57	58	39

tabel 1e. isolatiewaarden dubbel glas gasgevuld (xx = gelamineerd glas)

Over het algemeen is het geluidveld bij gevels aan de voorzijde niet diffuus, zodat de formules (5) en (6) niet zomaar toegepast kunnen worden. Figuur 2 schetst de situatie voor een vlakke golf, invallend onder een hoek θ. Het binnenkomende akoestisch vermogen wordt berekend op dezelfde wijze als bij formule (2); men dient alleen te letten op het type geluidveld aan de zendkant.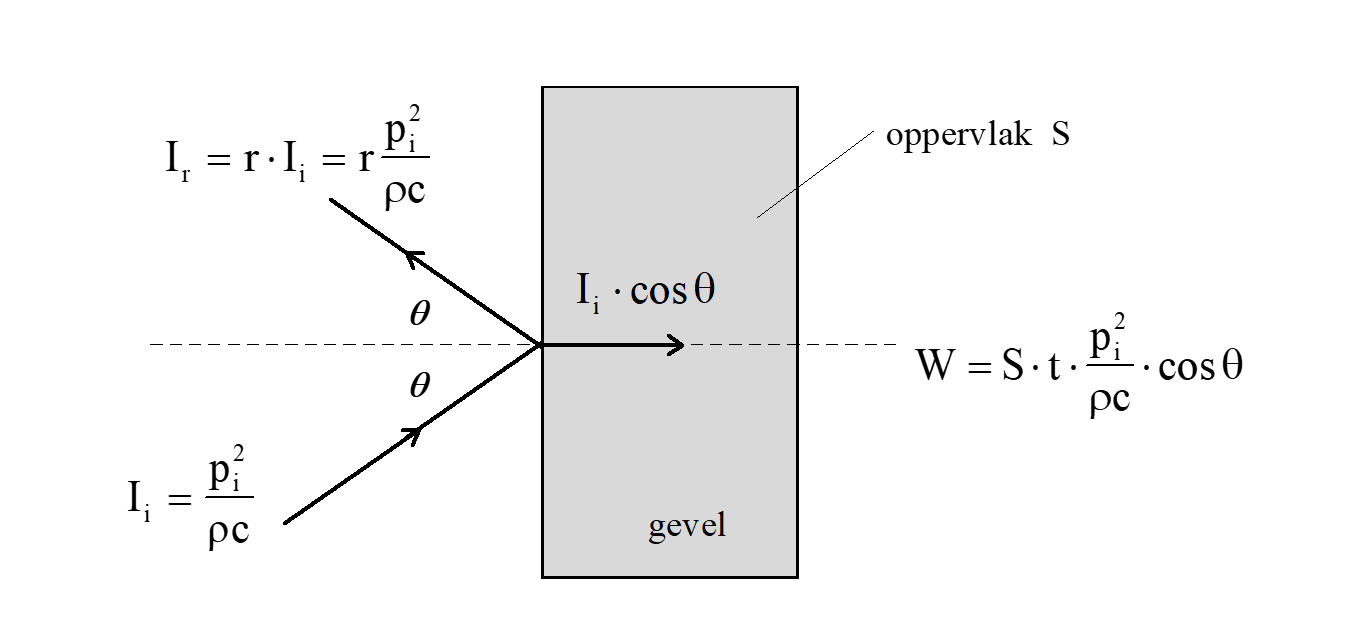 A diagram of a mathematical equation AI-generated content may be incorrect.

figuur 2. Weerkaatsing in een geluidgolf tegen een gevel

Veronderstellen we weer een diffuus geluidveld aan de ontvangkant, dan zal in analogie met (5) gelden:

(7) $\begin{equation*} R_{\text{lu},\theta} = 10 \log \left( \frac{p_i^2}{p_0^2} \right) - L_{\text{ontv}} + 10 \log \left( \frac{4S \cdot \cos \theta}{A_{\text{ontv}}} \right) \end{equation*}$

Echter, het geluiddrukniveau aan de zendkant L_zend is samengesteld uit het geluiddrukniveau van zowel de invallende als de gereflecteerde golf:

(8) $\begin{equation*} L_{\text{zend}} = 10 \log \left( \frac{p_i^2}{p_0^2} + r \cdot \frac{p_i^2}{p_0^2} \right) = 10 \log \frac{p_i^2}{p_0^2} + 10 \log (1 + r) \end{equation*}$

zodat formule (7) geschreven moet worden als:

(9) $\begin{equation*} R_{\text{lu}, \theta} = L_{\text{zend}} - L_{\text{ontv}} + 10 \log \left( \frac{4 S \cdot \cos \theta}{(1 + r) \cdot A_{\text{ontv}}} \right) \] \end{equation*}$

Let wel op: in deze formule is cosθ een gevolg van het “normaliseren” van L_zend. Het wil hier niet zeggen, dat R_lu,θ afneemt met θ .

Auteurs

ir. L. Nederlof

prof.ir. J.J.M. Cauberg

Niveau

bachelor

master

Genormaliseerde luchtgeluidisolatie

Auteurs

Niveau

Tags

Onze partners

Over Klimapedia