A017

Luchtgeluidisolatie – Coïncidentie-effect

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Figuur 1 toont sterk uitvergroot hoe het oppervlak van een plaat vervormd wordt door de opeenvolgende golffronten van een invallende, vlakke, lopende golf. Door het voortschrijdende karakter daarvan ontstaat aan het oppervlak van de plaat een gedwongen buiggolf, die zich met een snelheid c_opp daarlangs voortplant.

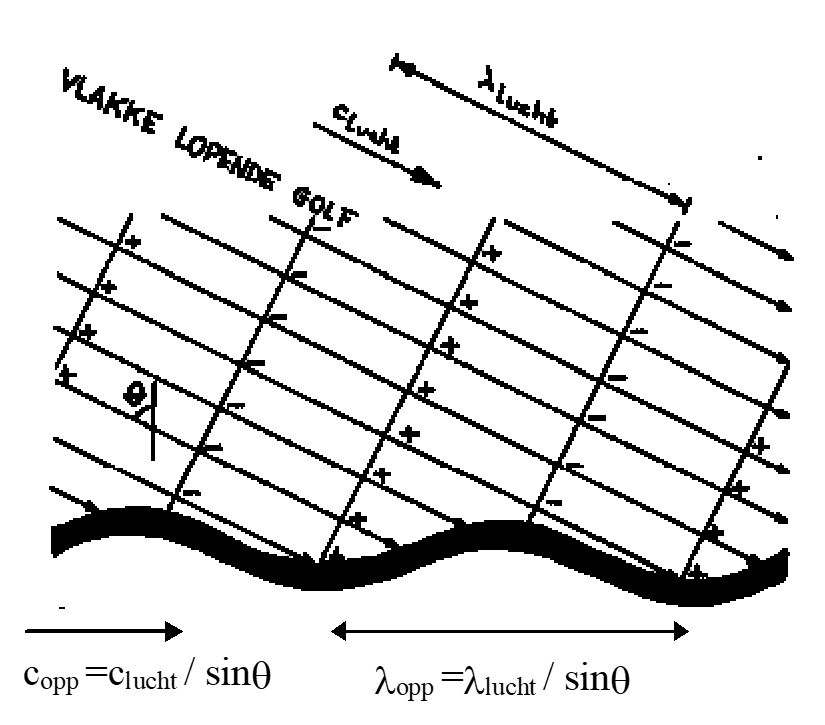
A diagram of a golf course AI-generated content may be incorrect.

figuur 1. opwekking van gedwongen buiggolf door invallende, vlakke, lopende golf

Beschouwen we een vast punt op het oppervlak, dan is het alsof daar ter plaatse de plaat met een puntbelasting wordt aangestoten. Vanuit zo’n punt planten zich dan vrije, rechte buiggolven door het materiaal voort. Dit type golven treedt eveneens op bij contactgeluid, met als typisch voorbeeld naaldhakken op een stenen vloer. Voor vrije buiggolven bestaat de golfvergelijking uit een differentiaalvergelijking van de vierde orde. We kunnen hier volstaan met de formule voor de voortplantingssnelheid van vrije, rechte buiggolven:

(1) $\begin{equation*} c_{\text{vrij}} = \sqrt[4]{\frac{K d^2 \cdot 4 \pi^2 f^2}{12 \rho}}\ [\text{m/s}] \end{equation*}$

Waarin:
K = dynamische elasticiteitsmodulus [N/m²]
d = dikte van de plaat [m]
ρ = dichtheid van het plaatmateriaal [kg/m³]
f = frequentie van de belasting [Hz]

Er treden dus zowel gedwongen als vrije buiggolven in de plaat op, die zich elk met een eigen snelheid voortplanten. Indien nu beide snelheden aan elkaar gelijk zijn, en de bijbehorende vervormingen steeds samenkomen, spreekt men van coïncidentie. Naar de aard van dit verschijnsel kunnen we daarbij een aanzienlijke vermindering van de geluidisolatie verwachten.

De coïncidentievoorwaarde luidt dus c_vrij=c_opp=c_lucht/sin(θ) en aangezien c_lucht≈340m/s kunnen we uit formule (1) afleiden bij welke frequentie coïncidentie optreedt ofwel de coïncidentiefrequentie:

(2) $\begin{equation*} f_c = \frac{64 \cdot 10^3}{\sin^2 \theta \cdot d \cdot \sqrt{K/\rho}} [\text{Hz}] \end{equation*}$

Bij loodrechte inval (θ = 0⁰) zal géén coïncidentie waargenomen worden (f_c→∞). De laagste frequentie waarbij nog coïncidentie op kan treden, ligt bij θ =90⁰ en is de grensfrequentie:

(3) $\begin{equation*} f_{\text{grens}} = \frac{64 \cdot 10^3}{d \cdot \sqrt{K/\rho}} [\text{Hz}] \end{equation*}$

Onder de grensfrequentie kan dus eveneens géén coïncidentie optreden. Daarbij moet wel bedacht worden, dat de coïncidentievoorwaarde een limietsituatie vertegenwoordigt, zodat we in werkelijkheid al enig effect kunnen verwachten in het frequentiegebied onder f_grens.

Een typisch praktijkgeval van coïncidentie kan optreden bij hoogbouw langs een verkeersweg: op hogere verdiepingen kan de invalshoek van het geluid op een gevel zodanig zijn, dat precies aan de coïncidentievoorwaarde wordt voldaan (zie figuur 2a+b).

Tabel 1 geeft de grensfrequentie voor onder andere de plaatconstructies van figuur 2 (module A-16; “Luchtgeluidisolatie – massawetten voor enkelbladige constructies”); het coïncidentiegebied blijkt nu overeen te komen met het gebied, waar de isolatiecurve in toenemende mate afwijkt van de theoretische massawet.

	d [mm]	ρ [kg/m³]	K [N/m²]	f_grens[Hz]
Staalplaat	3,5	7800	210.10⁹	3500
Spaanplaat	36	650	3.10⁹	800
Spiegelglas	6	2500	70.10⁹	2000
betonplaat	100	2000	20.10⁹	200

tabel 1. grensfrequentie (afgerond) bij enkele plaatvormige constructies

De ernst van het coïncidentie-effect hangt natuurlijk nauw samen met de mate waarin buiggolven uitdempen in een constructie. Dit wordt uitgedrukt in een verliesfactor voor buiggolven η, die voor een bepaalde frequentie f kan worden afgeleid uit de (gemeten) mechanische nagalmtijd T_mech van een constructie volgens:

(4) $\begin{equation*} \eta = \frac{2,2 \cdot T_{\text{mech}}}{f} \quad [\text{met } 0 \leq \eta \leq 1] \end{equation*}$

In η worden alle dempingsmechanismen meegenomen, te weten:

demping van buiggolven in het materiaal zelf (wrijvingsverliezen);
inklemming aan de randen (randverliezen);
geluidafstraling naar de omgeving (impedantieverliezen).

Hierdoor is η ook geen materiaalconstante, maar een constructie-eigenschap; die dan ook beïnvloed wordt door de wijze van uitvoering. Voor een bepaald type constructie kan weliswaar met een gemiddelde η gerékend worden, maar een geméten isolatiecurve zal onherroepelijk de spreiding in η weerspiegelen.

De grootte van η ligt meestal in orde van één of enkele procenten.

Hier wordt volstaan met het vermelden van de transmissiecoëfficiënt (t) als de gekwadrateerde modulus van de complexe overdrachtsfunctie, waarbij:

(5) $\begin{equation*} \frac{1}{t} = \left| (1 + j) \frac{\pi f m \cos \theta}{\rho c} \left[ 1 - (1 + j \eta) \frac{f^2}{f_{\text{grens}}^2} \sin^4 \theta \right] \right|^2 \end{equation*}$

Voor voldoende lage frequenties (f<<f_grens ) gaat formule (5) vrijwel over in formule (6) (module A-16; “Luchtgeluidisolatie – massawetten voor enkelbladige constructies”) en lijkt de theoretische massawet dus wel degelijk adequaat; ook bij alzijdige inval.

Bij de coïncidentiefrequentie (f=f_c=f_grens/sin²θ ) vinden we uit formule (5):

(6) $\begin{equation*} \frac{1}{t_c} = \left| 1 + \frac{\pi f_c m \cos \theta}{\rho c} \cdot \eta \right|^2 \end{equation*}$

Zodat ten opzichte van de theoretische massawet de geluidisolatie bij coïncidentie circa 20.logη lager uitkomt. Als er geen dempingsverliezen zijn (η=0), zakt de geluidisolatie in dat geval zelfs terug tot 0 dB.

Figuur 2a brengt het verloop van de isolatiecurve in beeld op basis van formule (5) voor een oneindig uitgestrekte glasplaat van 6mm dikte. De coïncidentie-dip bedraagt hier globaal 20.log(0,01)=40 dB. Bij eindige platen zullen ook de randverliezen een rol gaan spelen, η navenant groter worden en het isolatieverlies geringer. In figuur 2b is de situatie weergegeven bij een betonplaat van 100mm: het isolatieverlies door coïncidentie treedt nu op bij veel lagere frequenties en valt midden in het frequentiespectrum van verkeerslawaai.

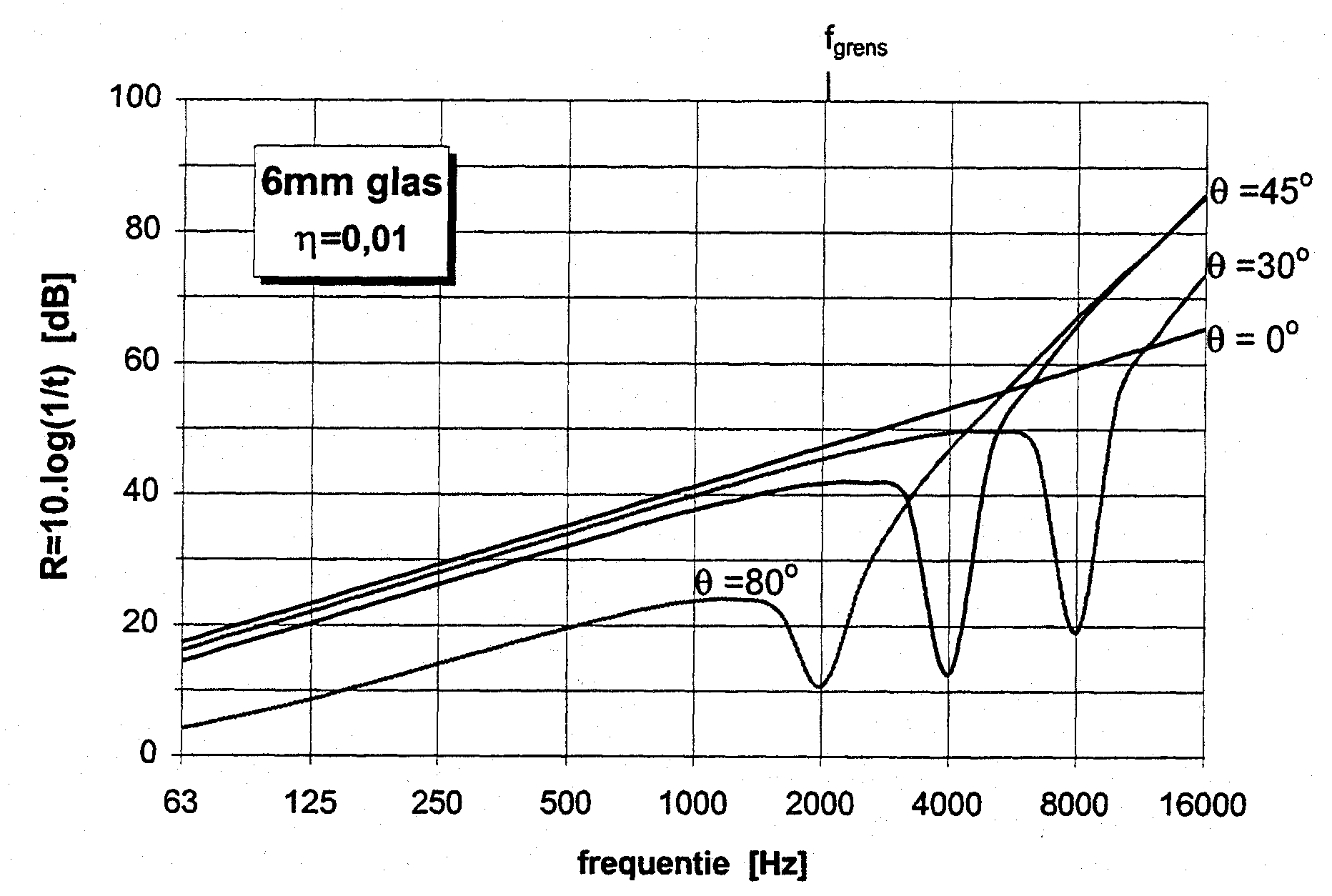
figuur 2a. coïncidentie-effect bij 6mm glas voor diverse invalshoeken

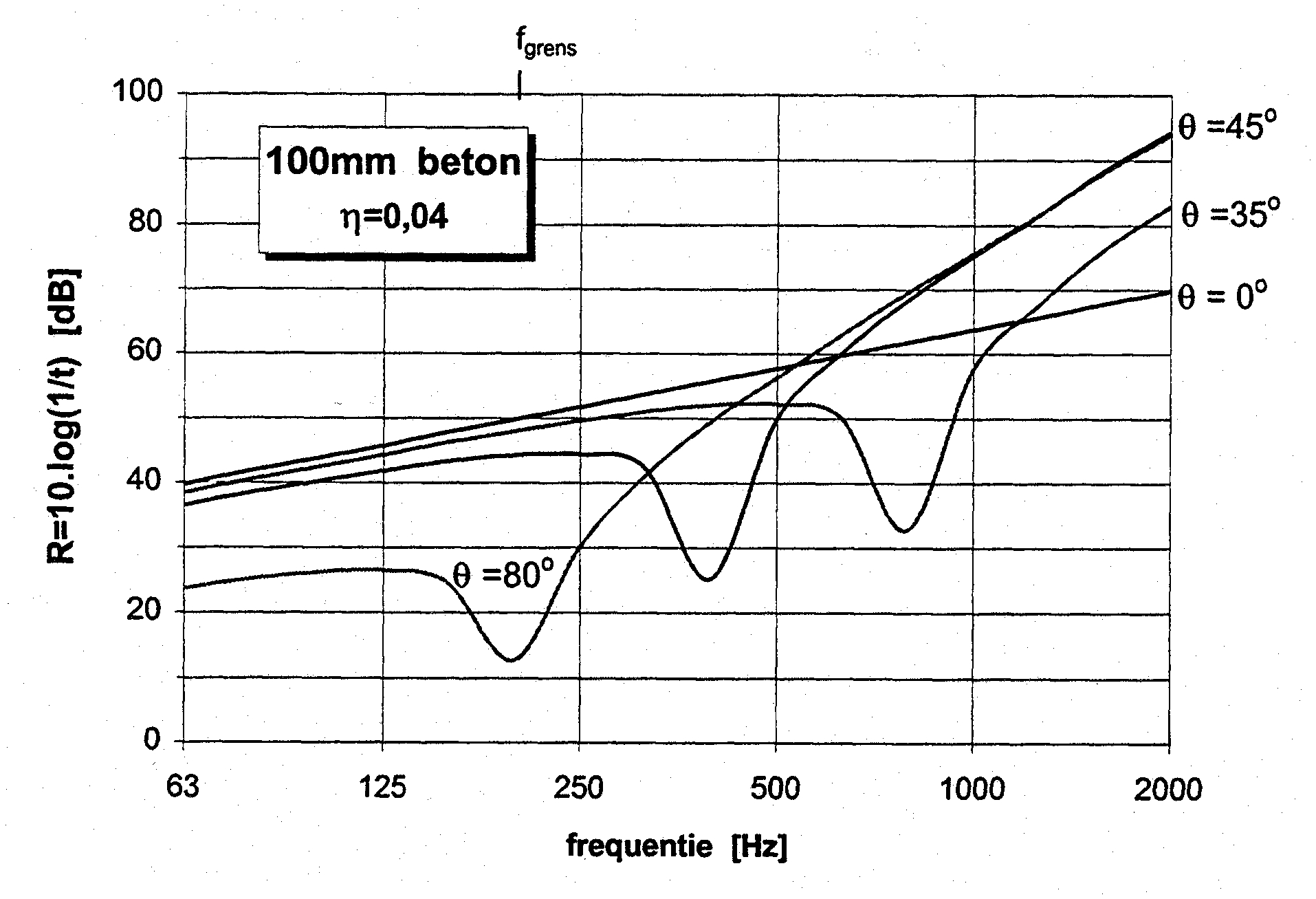
figuur 2b. coïncidentie-effect bij 100mm beton voor diverse invalshoeken

De grafieken van figuur 2 mogen niet verkeerd geïnterpreteerd worden: coïncidentie verdwijnt niet met een afnemende invalshoek, maar verschuift naar hogere frequenties. Men moet zich ook niet blind staren op het feit, dat voor één specifieke hoek van inval de isolatiecurve zich bij hogere frequenties herstelt en zelfs boven de theoretische massawet voor loodrechte inval (θ=0⁰) uitkomt. De geringe isolatie bij f<f_grens en grotere invalshoek (zie θ=80⁰ in figuur 1; module A-16; “Luchtgeluidisolatie – massawetten voor enkelbladige constructies”) is conform de voorspelling van formule (8; dezelfde module). Dit effect van de invalshoek zet zich voort bij f>f_grens en de hoogst liggende curve wordt ongeveer bereikt voor θ≈60⁰. In de praktijk hebben we meestal te maken met alzijdig invallend geluid en een breed spectrum van frequenties, zodat er een heel gamma aan coïncidenties mogelijk is. Een gemeten isolatiecurve laat het resulterend effect hiervan zien en dat wordt in hoge mate bepaald door de zwakste schakel: díe combinaties van invalshoek en frequentie uit het aangeboden geluid, die juist wel aan de coïncidentievoorwaarde voldoen. Als gevolg hiervan verloopt de isolatiecurve voor alzijdig invallend geluid vanaf de grensfrequentie effectief met circa 7,5 dB/octaaf; veel lager dus dan in figuur 2 is te zien, namelijk 18 dB/octaaf volgens formule (5).

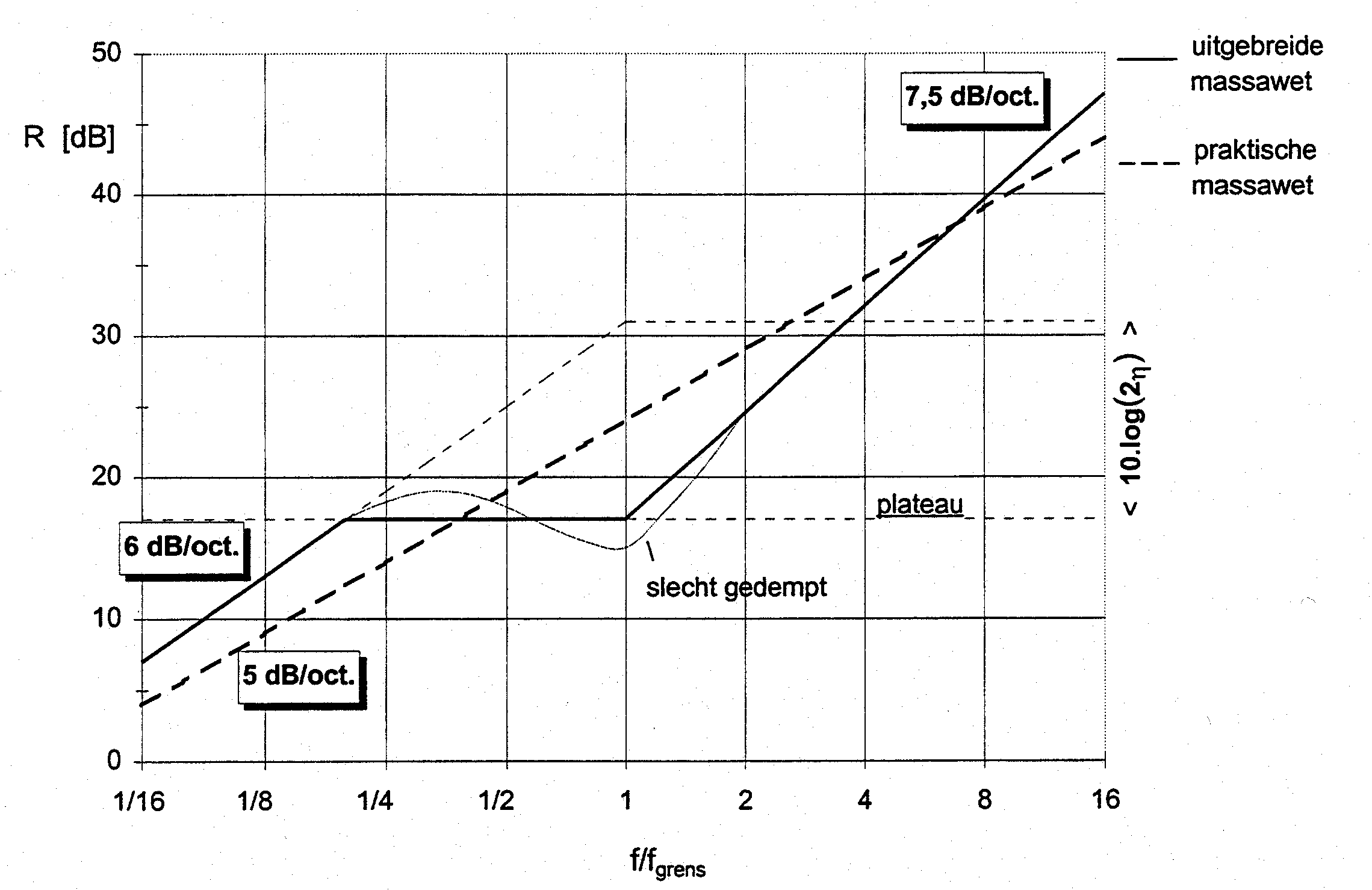
figuur 3. verloop van de isolatiecurve bij alzijdige inval en massa m ≤ 70 kg/m² voor m >70 kg/m² schuift het horizontale plateau 20·log(m/70) omhoog

De isolatiecurve voor alzijdig invallend geluid kan nu op de hierna volgende wijze worden benaderd, kortheidshalve aan te duiden als de uitgebreide massawet.

Voor het laagfrequentgebied waarin f<<f_grensgeldt de theoretische massawet voor alzijdige inval, zodat:

(7) $\begin{equation*} R_{\text{LF}}= R_\perp - 5 = 20 \log m + 20 \log \frac {f}{500} + 7 \end{equation*}$

Plateaugebied, globaal beginnend bij $f_{\text{grens}} = \sqrt{2 \eta}$ met een horizontaal verloop:

(8) $\begin{equation*} R_{PL} = R_{\perp}(f_{\text{grens}}) - 5 + 10 \log (2 \eta) \end{equation*}$

Het plateau begint dus al beneden f_grens, waar echte coïncidentie nog niet op kan treden, maar de buiggolven al wel een rol spelen. Bij slechte demping zullen de isolatiewaarden enigszins om R_PL heen slingeren.

Bij hoogfrequentgebied f>>f_grens met asymptotische benadering volgens:

(9) $\begin{equation*} R_{HF} = R_{\perp}(f_{\text{grens}}) - 5 + 10 \log (2 \eta) + 25 \log \frac{f}{f_{\text{grens}}} \end{equation*}$

Voor massa’s boven 70 kg/m² wordt het plateau gecorrigeerd (opgetild) tot:

(10) $\begin{equation*} R_{\overset{*}{PL}} = R_{PL} + 20 \log \frac{m}{70} \end{equation*}$

Het horizontale deel schuift ook iets naar rechts, omdat de LF-benadering iets langer doorloopt en de HF-asymptoot wat verder voorbij f_grens bereikt wordt.

Figuur 3 brengt het voorgaande in beeld voor een massa van 70 kg/m², met ter vergelijking de praktische massawet. Hieruit blijkt dat de laatste globaal overeenkomt met een lineaire regressie over het totale frequentiegebied, waarbij de verliesfactor η min of meer wordt weggemoffeld.

Auteurs

ir. L. Nederlof

prof.ir. J.J.M. Cauberg

Niveau

bachelor

master

Luchtgeluidisolatie – Coïncidentie-effect

Auteurs

Niveau

Tags

Onze partners

Over Klimapedia