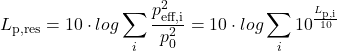KLIMAPEDIA

A002

Geluidwaarneming

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

De mens ervaart geluid op basis van twee aspecten: frequentie en geluidsterkte.

Hoe fraai, lelijk of complex geluid ook moge klinken, het bestaat uit een samenstel van afzonderlijke golven, elk met een eigen frequentie en amplitude, maar onderling in fase verschoven. Voor de totale momentane geluiddruk geldt het superpositie-beginsel:

(1) $\begin{equation*} p(t)=\sum_{i}\hat{p}_{i}sin(2\pi f_i t+\varphi_i) \end{equation*}$

Intuïtief zal men aanvoelen dat de geluidsterkte bepaald wordt door de geluiddruk, althans de amplitude daarvan. Fysiologisch begint het horen met een mechanische beweging van onderdelen van het gehoororgaan en komt de waarneming van geluidsterkte in feite neer op een overdracht van akoestische golfenergie, welke evenredig is met het kwadraat van de golfamplitude (formule (8) zie module A-1; Golfkarakter van geluid).

Als karakteristieke grootheid voor de geluidsterkte wordt daarom de effectieve geluiddruk over een periode t₂-t₁ gehanteerd, die gedefinieerd is als:

(2) $\begin{equation*} p_{\text{eff}}=\sqrt{\frac{1}{t_2-t_1}\int_{t_1}^{t_2}p^2dt} \end{equation*}$

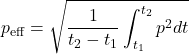
Eenvoudig valt aan te tonen dat voor een zuiver sinusvormige golf met frequentie f en amplitude $\hat{p_i}$ geldt: $p_{\text{eff}}=\frac{1}{2}\sqrt{2}\cdot\hat{p}$ indien t₂-t₁>>1/f (zie figuur 1).

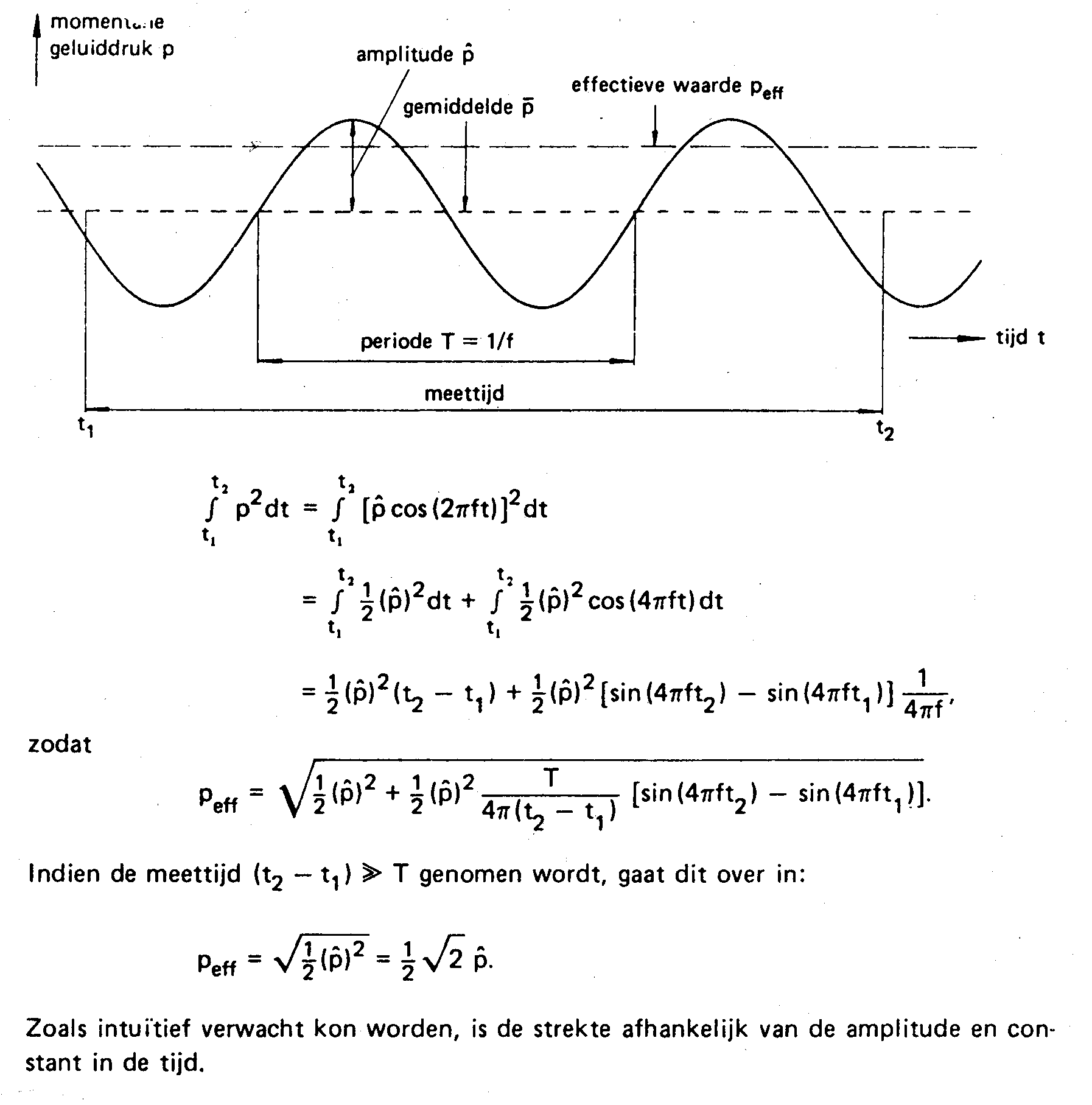
figuur 1. berekening van p_eff voor een sinusvormige toon op een vaste plaats

Op grond van (1) en (2) kan eveneens worden afgeleid dat voor samengesteld geluid, mits bestaande uit onderling ongecorreleerde golven, geldt:

(3) $\begin{equation*} p^{2}_{\text{eff,totaal}}=\sum_{i}p^{2}_{\text{eff,}i} \end{equation*}$

Ongecorreleerd wil zeggen $\frac{1}{t_2-t_1}\int_{t1}^{t2}p_ip_jdt=0$ voor elke combinatie van golven $i\neq j$ ; een situatie die zich praktisch altijd voordoet. Een geval waarbij dat niet zo is, kan bij voorbeeld optreden bij reflectie: rechtstreeks en gereflecteerd geluid zijn dan gecorreleerd door hun weglengteverschil d, zodanig dat p_j(x,t)=p_i(x,t+d/c). Afhankelijk van d zal (zie formule 2) dan waarden tussen 0 en 2p_eff,i opleveren; er is dan sprake van interferentie.

Uit metingen blijkt, dat jonge mensen een effectieve geluiddruk van 2.10^-5 Pa (»2.10^-10 atm!) bij 1000 Hz nog juist kunnen waarnemen. Echter, ons gehoororgaan is niet voor alle frequenties even gevoelig en met name bij lagere frequenties moet de amplitude veel groter zijn om dezelfde subjectieve geluidsterkte te ervaren (zie ook figuur 2).

Bij p_eff» 200 Pa kan beschadiging van het gehoororgaan optreden, zoals scheuren van het trommelvlies, en spreekt men van de pijngrens.

image.tif

figuur 2. geluiddrukniveaus in de dagelijkse omgeving — isofonen volgens ISO-R220 (1961)

De grote range in de optredende effectieve geluiddruk bij diverse geluiden heeft ertoe geleid dat in de akoestiek een handzamer maat voor de geluidsterkte is geïntroduceerd: het geluiddrukniveau L_pmet als eenheid de decibel (dB):

(4) $\begin{equation*} L_p=10log\frac{p^2_{\text{eff}}}{p^2_0} dB \end{equation*}$

Hierin is p₀ = 2.10^-5 Pa de zogenaamde referentiewaarde, overeenkomend met de effectieve geluiddruk van de eerder genoemde gehoordrempel bij 1000 Hz.

Voor enkele typische geluiden is in figuur 2 de ordegrootte van p_eff en L_p uitgezet.

Het begrip geluiddrukniveau is weliswaar fysisch een handzame grootheid, maar kent als maat voor de “hardheid” of “luidheid” van geluid toch beperkingen.

Uitgaande van een zuivere toon van 1000 Hz en een bepaald geluiddrukniveau kan men bepalen hoeveel het geluiddrukniveau bij andere frequenties moet bedragen om het daar als even “luid” te ervaren. Zo’n oorgevoeligheidsmeting geeft uiteraard individuele verschillen ten gevolge van fysionomie, leeftijd en eventuele gehoorbeschadigingen.

Figuur 2 toont zulke isofonen (lijnen van gelijk luidheidniveau), zoals vastgesteld door de “International Standardization Organization” in publicatie ISO-R220 uit 1961.

De krommen zijn geldig voor zuivere tonen in een vrij geluidveld, waargenomen met beide oren en met middeling over alle leeftijden; de aangegeven gehoordrempel ligt daardoor bij 1000 Hz niet op 0 dB.

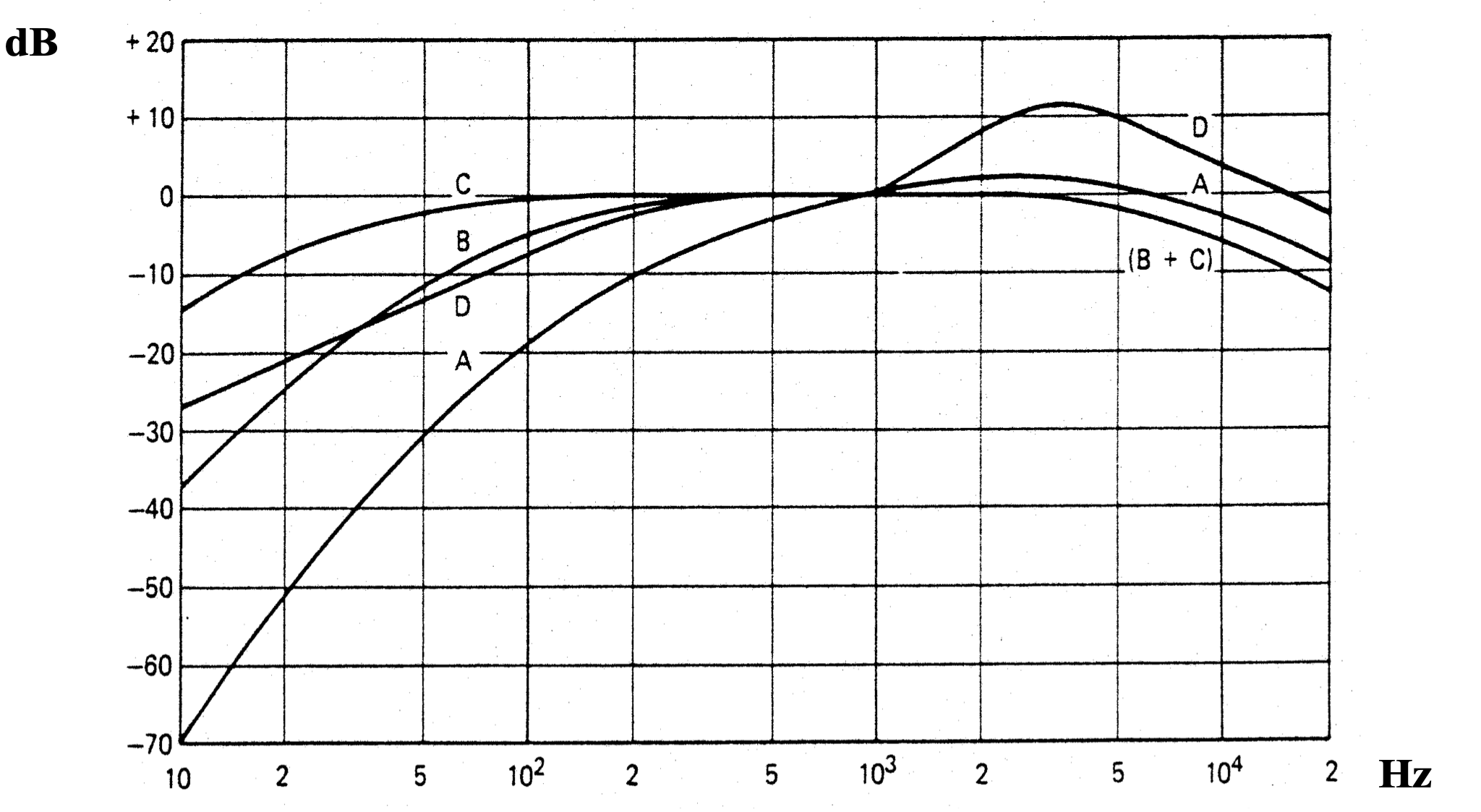
image.tif

figuur 3. weegfuncties A, B, C en D

Op grond van de oorgevoeligheid is het dus zinvol om bij de kwantificering van de mate van geluidhinder (sterkte) op enigerlei wijze de frequentie van het geluid mee te wegen. Dit komt neer op het inbouwen van een frequentie-afhankelijk referentieniveau p₀(f) in formule 4. Omdat isofonen niet equidistantieel verlopen (zie figuur 2) zou eigenlijk ook nog rekening moeten worden gehouden met de hoogte van het geluiddrukniveau, doch dit zou onherroepelijk tot niet-lineaire en dus onhandelbare formules leiden.

Men heeft een aantal weegfuncties gedefinieerd (figuur 3 en tabel 2), maar de meest gangbare is de A-weging, die leidt tot het geluidniveau L_A uitgedrukt in dB(A):

(5) $\begin{equation*} \begin{aligned} L_A=10log\frac{p^2_{\text{eff}}}{p^2_0(\text{f})} \text{[dB(A)]} = \\ =10log\frac{p^2_{\text{eff}}}{p^2_0}+10log\frac{p^2_0}{p^2_0(\text{f})}=L_P\text{[dB]}-10log\frac{p^2_0(\text{f})}{p^2_0} \end{aligned} \end{equation*}$

Formule (5) laat zien dat in een bepaald frequentiegebied het geluidniveau L_A in dB(A) uit het geluiddrukniveau L_pin dB is af te leiden (en omgekeerd) door middel van een correctieterm, die in feite het geluiddrukniveau in dB voorstelt van een fictieve, geïdealiseerde gehoordrempel.

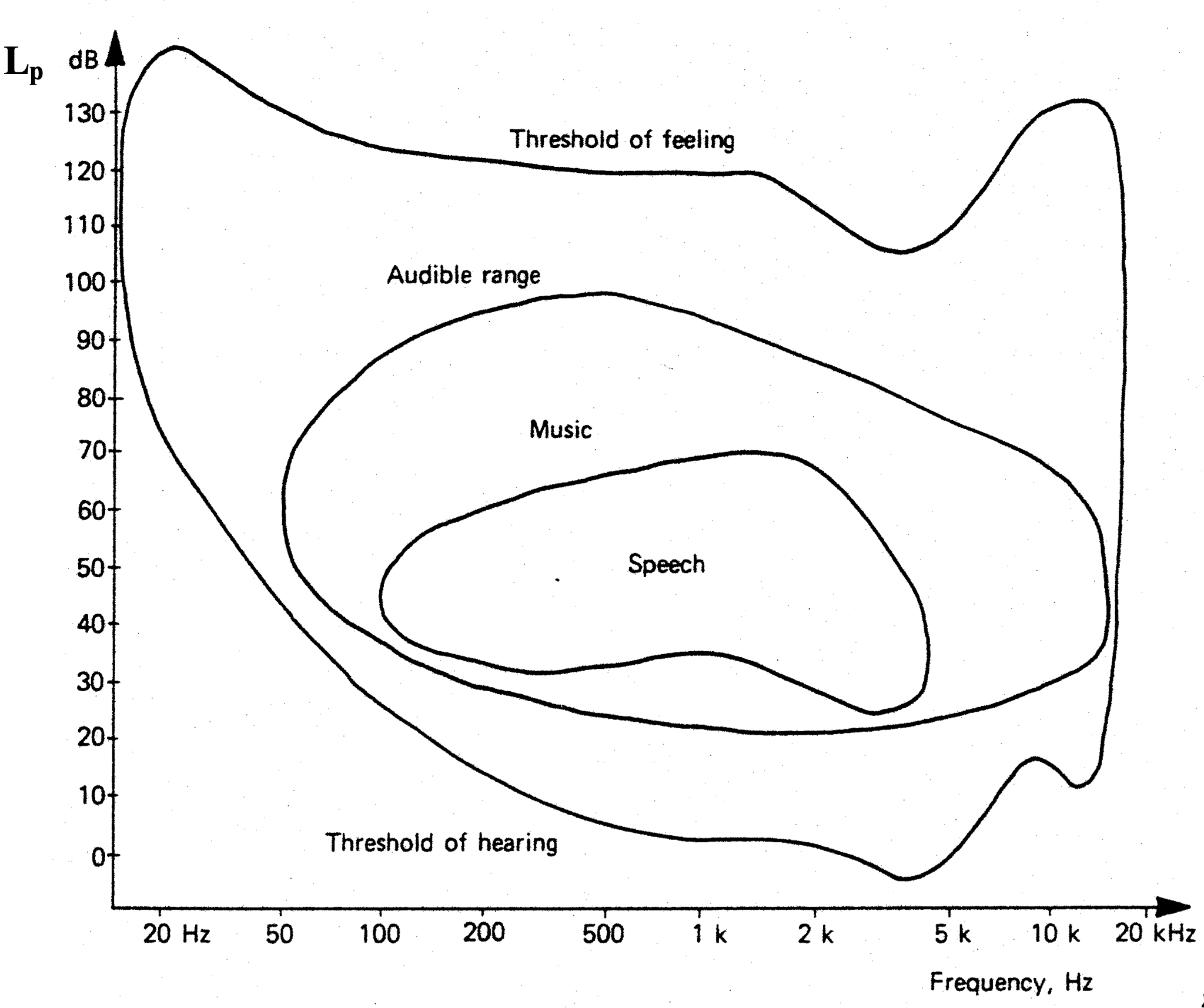
image.tif

figuur 4. enkele karakteristieke geluiden

Figuur 4 brengt de grenzen in beeld van het hoorbare geluid en die van spraak en muziek.

Het frequentiebereik van het menselijke gehoor ligt globaal tussen 16 Hz en 16000Hz en beslaat 10 octaven. Een octaafband is een frequentiegebied, dat omvat wordt door een ondergrens f₁ en bovengrens f₂, waarvoor per definitie geldt: f₂= 2·f₁.

Naast octaven kent men ook halve octaven ( $\text{f}_2=\sqrt{2}\cdot\text{f}_1$ ) en tertsen ( $\text{f}_2=\sqrt[3]{2}\cdot\text{f}_1$ ). Gebruikelijk is om zulke frequentiebanden aan te duiden met hun zogeheten middenfrequentie, gedefinieerd als:

(6) $\begin{equation*} \text{f}_m=\sqrt{\text{f}_2\cdot\text{f}_1} \text{[Hz]} \end{equation*}$

In de akoestiek hanteert men voor berekeningen en beoordelingen een reeks voorkeurfrequenties, die bij afspraak zijn vastgelegd als de middenfrequenties van de internationaal genormaliseerde octaafbanden van tabel 1.

octaafband nummer	frequentiegebied [Hz]	middenfrequentie [Hz]
1	45 – 90	63
2	90 – 180	125
3	180 – 355	250
4	355 – 710	500
5	710 – 1415	1000
6	1415 – 2830	2000
7	2830 – 5660	4000
8	5660 – 11320	8000

tabel 1. genormaliseerde octaafbanden

Elke octaafband kan weer onderverdeeld worden in drie genormaliseerde tertsbanden met middenfrequenties zoals in tabel 2.

Strikt genomen zijn de in tabel 2 opgenomen correctietermen voor de conversie van dB naar dB(A) alleen geldig voor de vermelde tertsbanden; echter, in de praktijk worden ze ook voor octaafbanden gebruikt.

frequentie [Hz]	A-weging	B-weging	C-weging	D-weging
50	-30,2	-11,6	-1.3	-13,6
63	-26,2	-9,3	-0,8	-11,6
80	-22,5	-7,4	-0,5	-9,6
100	-19,1	-5,6	-0,3	-7,8
125	-16,1	-4,2	-0,2	-6,0
160	-13,4	-3,0	-0,1	-4,4
200	-10,9	-2,0	0	-3,1
250	-8,6	-1,3	0	-1,9
315	-6,6	-0,8	0	-1,0
400	-4,8	-0,5	0	-0,3
500	-3,2	-0,3	0	0
630	-1,9	-0,1	0	-0,1
800	-0,8	0	0	-0,4
1000	0	0	0	0
1250	0,6	0	0	1,9
1600	1,0	0	0,1	5,4
2000	1,2	-0,1	0,5	8,0
2500	1,3	-0,2	0,3	10,0
3150	1,2	-0,4	0,5	11,0
4000	1,0	-0,7	0,8	10,9
5000	0,5	-1,2	-1,3	10,0
6300	-0,1	-1,9	-2,0	8,5
8000	-1,1	-2,9	-3,0	6,0
10000	-2,5	-4,3	-4,4	3,0

tabel 2. correctietermen voor de weegfuncties A, B, C en D – niveau in dB(A) = niveau in dB + tabelwaarde

Het totale geluiddrukniveau van diverse gelijktijdig optredende bronnen, volgt uit de energetische sommatie over de afzonderlijke niveaus L_p,i (substitueer formule 3 in formule 4); dit levert het zogenaamde resulterende geluiddrukniveau:

(7) $\begin{equation*} L_\text{p,res}=10\cdot log\sum_{i}\frac{p^2_{\text{eff,i}}}{p^2_0}=10\cdot log\sum_{i}10^{\frac{L_\text{p,i}}{10}} \end{equation*}$

Auteurs

ir. L. Nederlof

prof.ir. J.J.M. Cauberg

Niveau

bachelor

links

Nijsnet, Ruimteakoestiek voor architecten

Hogeschool van Amsterdam HZ University of Applied Sciences NHL Stenden Hogeschool Hanzehogeschool Groningen Hogeschool van Arnhem en Nijmegen Avans Hogeschool, Tilburg en Den Bosch De Haagse Hogeschool Hogeschool Utrecht Windesheim, Zwolle Hogeschool Inholland Alkmaar Technische Universiteit Delft Nederlands Vlaamse Bouwfysica Vereniging Stichting Kennisoverdracht Bouwfysica

Klimapedia is een kennisbank voor bouwfysica, binnenmilieu, installaties en duurzaamheid. Les- en kennismateriaal worden hier aangeboden van technische universiteiten, technische hoge scholen en vakgerichte cursussen. Docenten en cursusleiders kunnen hier hun dictaten, presentaties, toetsen, oefeningen en achtergrondinformatie delen en beschikbaar stellen voor collega’s, studenten en andere geïnteresseerden.

privacybeleid | Klimapedia maakt enkel gebruik van functionele cookies ten einde het gebruik van onze website in kaart te kunnen brengen. Dat gebeurt anoniem waarbij uw IP-adres wordt gemaskeerd. Wij maken gebruik van Matamo On-Premise waarbij de gegevens op onze eigen server beheerd en geanalyseerd worden. De geanonimiseerde gegevens zijn derhalve niet voor derde partijen zichtbaar.

Geluidwaarneming

Auteurs

Niveau

Tags

links

Onze partners

Over Klimapedia