A001

Golfkarakter van geluid

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Beweegt men een vlakke plaat in lucht periodiek heen en weer in de richting loodrecht op de plaat, dan zullen in de lucht afwisselend verdichtingen en verdunningen ontstaan zoals uitgebeeld in figuur 1.

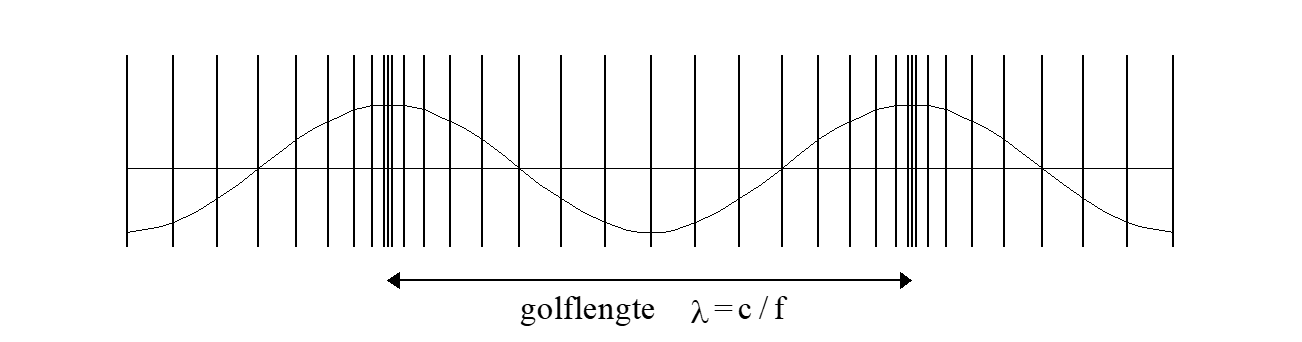
A graph of a function AI-generated content may be incorrect.

figuur 1. geluid als longitudinale golf

Men kan zich dat als volgt voorstellen. Als de plaat naar rechts beweegt, wordt daar de naastliggende lucht samengedrukt (verdicht). Deze drukverhoging werkt als een kracht op de verderop aanwezige lucht, die hierdoor in beweging komt en op haar beurt weer wordt samengedrukt. Wordt de plaat vervolgens naar links bewogen, dan zal de lucht ter rechterzijde in eerste instantie nog in haar beweging naar rechts volharden, zodat er een verdunning naast de plaat ontstaat en dus een onderdruk, die op de lucht weer een kracht naar links zal uitoefenen, ad infinitum.

Als de uitwijking van de plaat en de herhalingsfrequentie voldoende groot zijn, dan kan men deze dichtheidsfluctuaties horen en is er sprake van geluid.

Fysisch spelen er twee balansmechanismen:

de krachtenvergelijking op grond waarvan het medium in beweging komt;
het continuïteitsprincipe, dat de dichtheid in een bewegend medium beschrijft.

Een uitgebreide en formele uitwerking hiervan is onder andere te vinden in “Geluidbeheersing/Soundcontrol” [1]. In deze module zal een iets andere en eenvoudiger aanpak worden gevolgd.

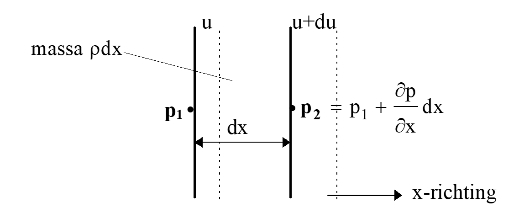
A diagram of a mathematical equation AI-generated content may be incorrect.

figuur 2. longitudinale verplaatsing

Beschouw nu een dun luchtplakje ter grootte van 1m², met dikte dx en massa ρ·dx (figuur 2), waarbij de druk links en rechts op p₁ respectievelijk p₂ wordt gesteld.

De druk p en deeltjessnelheid v zijn functies van plaats en tijd:

p= p(x,t) en v = v(x,t)

Als x en t variëren met dx respectievelijk dt, dan variëren p en v over het algemeen volgens:

dp= ∂p/∂x·dx + ∂p/∂t·dt en dv= ∂v/∂x·dx + ∂v/∂t·dt

Voor de beweging van het luchtplakje onder invloed van het drukverschil p₂-p₁, bedenken we dat het steeds om een verschil in momentane waarden gaat, zodat geldt:

p₁-p₂ = -dp = – ∂p/∂x·dx

Als dx maar klein genoeg is, mag aangenomen worden dat de snelheid aan beide zijden van het luchtplakje nagenoeg gelijk is, met andere woorden:

dv≈ ∂v/∂t·dt

Toepassing van de wet van Newton (kracht=massa x versnelling) levert dan voor 1 m² van zo’n luchtplakje de volgende vergelijking op:

– ∂p/∂x·dx = ρ·dx · dv/dt ≈ ρ·dx · ∂v/∂t

Zodat:

(1) $\begin{equation*} \frac{\partial p}{\partial x} = -\rho \cdot \frac{\partial v}{\partial t} \end{equation*}$

Voor het continuïteitsbeginsel gaan we hier uit van een luchtveer met lengte dx, waarvan de uiteinden zich over een afstand u respectievelijk u+du verplaatsen, en passen daarop de “wet van Hooke” toe:

(2) $\begin{equation*} p = -K \cdot \frac{\partial u}{\partial x} \end{equation*}$

Waarbij:
$\frac{\partial u}{\partial x}$ = de specifieke rek, waarbij u de verplaatsing van de luchtdeeltjes is.
K = de compressiemodulus of dynamische elasticiteitsmodulus in kg/ms²

Per definitie geldt v=∂u/∂t en differentiëren van formule 2 naar de tijd geeft dan:

(3) $\begin{equation*} \frac{\partial p}{\partial t} = -K \cdot \frac{\partial v}{\partial x} \end{equation*}$

Partieel differentiëren van (1) en (3) naar x respectievelijk t leidt dan via eliminatie van de mengterm ∂²v/∂x∂t tot de golfvergelijking voor geluid:

(4) $\begin{equation*} \frac{\partial^2 p}{\partial t^2} = \frac{K}{\rho} \cdot \frac{\partial^2 p}{\partial x^2} = c^2 \cdot \frac{\partial^2 p}{\partial x^2} \end{equation*}$

Gebruikelijk is om de vergelijking te schrijven met c² waarin dan voor de constante c, dit is de “voortplantingssnelheid” van de golf, geldt:

(5) $\begin{equation*} c = \sqrt{\frac{K}{\rho}}. \end{equation*}$

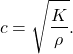
Voorgaande differentiaalvergelijking geldt, vanwege het eendimensionale karakter, slechts voor zogenaamde vlakke lopende golven.

De afleiding is in zoverre ook een vereenvoudiging van de werkelijkheid, dat geen rekening is gehouden met het feit dat compressie van lucht onvermijdelijk gepaard gaat met warmteontwikkeling ten gevolge van inwendige wrijving. Een deel van de met een geluidgolf getransporteerde (akoestische) energie wordt daardoor irreversibel omgezet in warmte, hetgeen uiteindelijk (gelukkig!) tot volledige uitdemping van het geluid leidt.

Golfvergelijking (4) heeft twee periodieke oplossingen, die behoren bij een voortplanting in positieve danwel negatieve x-richting:

(6) $\begin{equation*} p = p(t \pm \frac{x}{c}) = \hat{p} \cdot e^{j\omega(t \pm \frac{x}{c})} \end{equation*}$

Waarbij:
$\hat{p}$ = de amplitude van de golf
c = de voortplantingssnelheid van de golf
$\omega$ = de hoekfrequentie waarmee de momentane geluiddruk fluctueert, gerelateerd aan de geluidfrequentie (f) of toonhoogte via ω=2π·f

Partieel differentiëren van (1) en (3) naar t respectievelijk x, en eliminatie van de mengterm ∂²p/∂x∂t leidt tot een identieke golfvergelijking: ∂²v/∂t² = c²·∂²v/∂x²

Voor de deeltjessnelheid zal dus ook een functie analoog aan (6) gelden:

(7) $\begin{equation*} v = v\left(t \pm \frac{x}{c}\right) = \hat{v} \cdot e^{j\omega\left(t \pm \frac{x}{c}\right)} \end{equation*}$

Kenmerkend voor geluidgolven is, dat de voortplantingsrichting samenvalt met de bewegingsrichting van de mediumdeeltjes: ze hebben een longitudinaal karakter.

Men zou wellicht een faseverschil verwachten tussen geluiddruk en deeltjessnelheid, doch uit (1) volgt dat moet gelden:

(8) $\begin{equation*} p = \rho c \cdot v \end{equation*}$

Waarbij:
$\rho$ c = de specifieke akoestische golfweerstand of golfimpedantie

Op een willekeurige tijd en plaats heeft de golfenergie twee componenten: kinetische energie van de luchtdeeltjes en potentiële energie van de samengedrukte lucht(-veer). Gebruikmakend van de relaties (5) en (8), schrijven we voor de momentane energie per eenheid van volume, dit is de energiedichtheid van een (vlakke) golf:

(9) $\begin{equation*} E(t) = \frac{1}{2} \rho v^2 + \frac{1}{2} \frac{p^2}{K} = \frac{p^2}{\rho c^2} [\mathrm{J/m^3}] \end{equation*}$

Voorgaande beschouwing gaat weliswaar uit van lucht als medium, maar gezien de optredende parameters zou een en ander evengoed voor een ander medium kunnen gelden.

Geluidgolven kunnen inderdaad ook in andere materialen optreden, uiteraard met een andere voortplantingssnelheid $c = \sqrt{\frac{K}{\rho}}$ en andere golfimpedantie $\rho$ c (tabel 1).

De akoestische golfimpedantie speelt een rol bij de overgang van geluid van het ene medium naar het andere en bepaalt de mate van reflectie daarbij.

Is lucht het voortplantingsmedium, dan kan voor adiabatische omstandigheden en kleine drukvariaties de compressie-modulus afgeleid worden uit de ideale gaswet:

(10) $\begin{equation*} K = \frac{c_p}{c_v} \cdot P_0 [\mathrm{N/m^2}] \end{equation*}$

Waarbij:
P₀= de atmosferische druk (1 atm ≈ 10⁵ Pa);
c_P= specifieke warmte bij constante druk in J/kg K;
c_V= specifieke warmte bij constant volume in J/kg K;
c_P/c_V≈ 1,4 voor lucht.

De dichtheid van lucht bij 20 °C is 1,2 kg/m³, zodat de voortplantingssnelheid van geluid c≈340 m/s bedraagt en de golfimpedantie ρc =1,2·340 ≈ 410 kg/m²s.

materiaal	dyn. elast.modulus K [N/m²]	dichtheid ρ [kg/m³]	$c = \sqrt{\frac{K}{\rho}}$ [m/s]
lucht	14.10⁴	1,2	340
kurk	62.10⁹	250	498
gevelklinker	25.10⁹	2100	3450
kalkzandsteen	25.10⁹	2000	3536
grindbeton K300	35.10⁹	2400	3819
grindbeton K225	20.10⁹	2200	3015
lichtbeton (hollith)	28.10⁹	1700	4058
drijfsteen	5.10⁹	1000	2236
gipsplaten	4.10⁹	800	2236
gips	7.10⁹	700	3162
staal	210.10⁹	7800	5189
aluminium	70.10⁹	2800	5000
lood	17.10⁹	12200	1180
spiegelglas	70.10⁹	2500	5292
vurenhout	10.10⁹	470	4613
grenenhout	11.10⁹	520	4599
rode merantie	10.10⁹	600	4082
triplex oregon pine	12.10⁹	580	4549
Spaanplaat	3.10⁹	650	2148
hardboard (normaal hard)	4.10⁹	1000	2000
hardboard (half hard)	3.10⁹	650	2148

tabel 1. voortplantingssnelheid van geluid in diverse media

Om het dempingsmechanisme bij geluidoverdracht in rekening te brengen, zal (formule (1)) uitgebreid moeten worden met een term voor wrijvingsverliezen. We zullen hier volstaan met een aanpassing van formule (6), zodanig dat de amplitude van de golf exponentieel afneemt met de afstand:

(11) $\begin{equation*} p= p(t, x) = \hat{p} \cdot e^{-\alpha x} \cdot e^{j\omega \left(t \pm \frac{x}{c} \right)} \end{equation*}$

Waarbij:
α = de dempingsconstante per meter met orde van grootte 10^-3 [m^-1].

Luchtdemping is weliswaar een wezenlijk element in de geluidoverdracht, doch wordt pas significant op wat grotere afstanden en speelt daarom pas een rol in de akoestiek van grote ruimten en bij verkeerslawaai.

Dit betekent ook, dat in een beperkt gebied rond een bepaald punt van het geluidveld $\hat{p} \cdot e^{-\alpha x}$ ≈ constant is, zodat voorgaand golfmodel toch een adequate benadering blijft.

Voor een (moleculaire) beschouwing hoe de dempingsconstante α samenhangt met de frequentie, temperatuur, viscositeit en luchtvochtigheid wordt verwezen naar [1].

Ondanks de eenvoudige modellering kunnen we hier toch al concluderen, dat de overdracht van geluid in het vrije veld beïnvloed zal worden door de:

luchttemperatuur;
barometrische druk;
luchtvochtigheid (zeker bij mist);
aanwezigheid van luchtlagen met verschillende temperatuur (inversie);
wind.

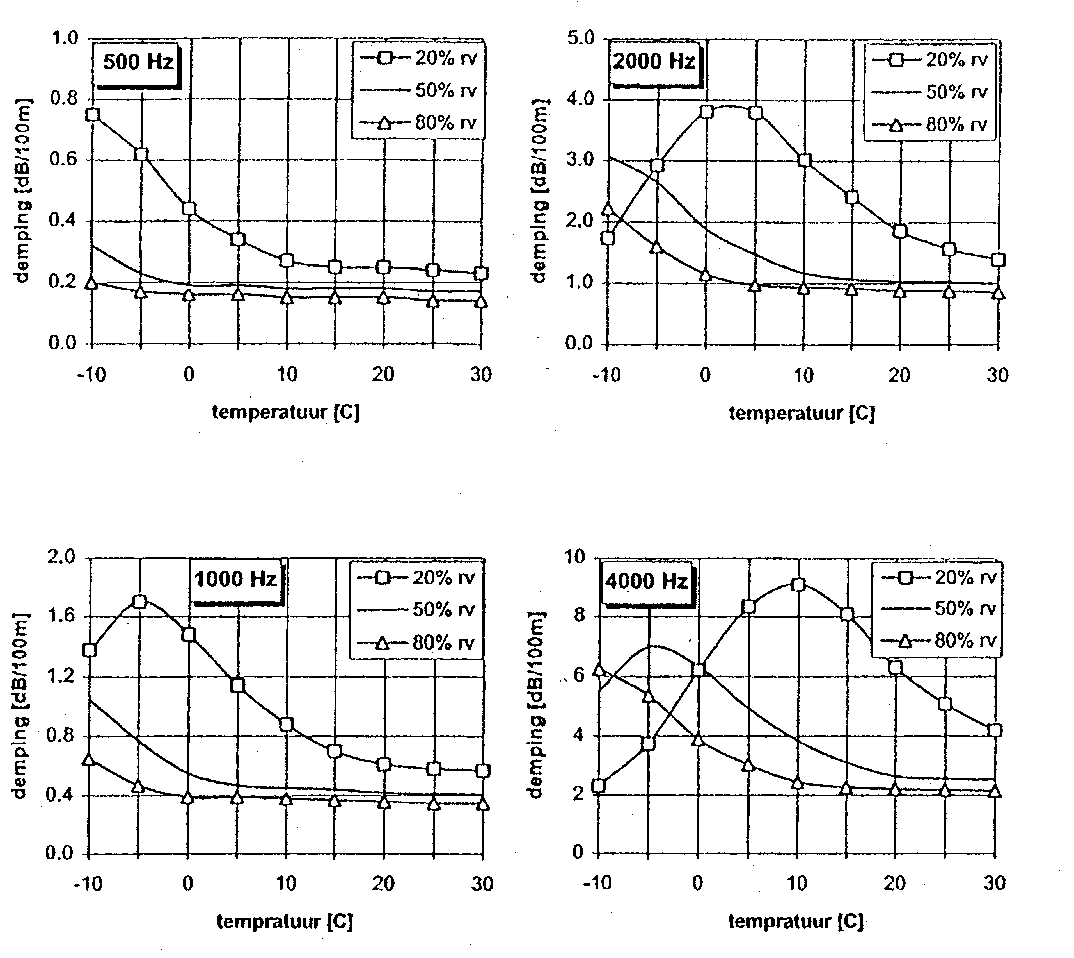
figuur 3. luchtdemping als functie van de frequentie en de luchttemperatuur

Literatuur

A.J. Berkhout, M.M. Boone, D. de Vries “Geluidbeheersing/Soundcontrol”, collegedictaat c36d, vakgroep Akoestiek, TU Delft.

Auteurs

ir. L. Nederlof

prof.ir. J.J.M. Cauberg

Niveau

bachelor

master

links

Nijsnet, Ruimteakoestiek voor architecten

Hogeschool van Amsterdam HZ University of Applied Sciences NHL Stenden Hogeschool Hanzehogeschool Groningen Hogeschool van Arnhem en Nijmegen Avans Hogeschool, Tilburg en Den Bosch De Haagse Hogeschool Hogeschool Utrecht Windesheim, Zwolle Hogeschool Inholland Alkmaar Technische Universiteit Delft Nederlands Vlaamse Bouwfysica Vereniging Stichting Kennisoverdracht Bouwfysica

Klimapedia is een kennisbank voor bouwfysica, binnenmilieu, installaties en duurzaamheid. Les- en kennismateriaal worden hier aangeboden van technische universiteiten, technische hoge scholen en vakgerichte cursussen. Docenten en cursusleiders kunnen hier hun dictaten, presentaties, toetsen, oefeningen en achtergrondinformatie delen en beschikbaar stellen voor collega’s, studenten en andere geïnteresseerden.

Golfkarakter van geluid

Literatuur

Auteurs

Niveau

Tags

links

Onze partners

Over Klimapedia