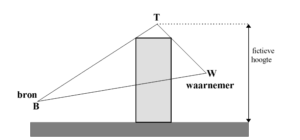
Onder schermwerking verstaan we niet alleen de reductie van het geluidniveau door het plaatsen geluidschermen, maar ook de afschermde werking van gebouwen. Gebouwen kunnen worden opgevat als een geluidscherm met een zekere “breedte”, waardoor in het “schermmodel volgens Maekawa” [1] met een fictieve hoogte gerekend wordt (figuur 1).
figuur 1. schermmodel: weglengteverschil δ=BT+TW-BW >0
Maekawa’s model is niet zozeer gebaseerd op de omweg, die het geluid ten gevolge van een obstakel moet maken, als wel op het verschijnsel van diffractie, dit is de buiging van het golffront om een obstakel heen. Het verschijnsel is vergelijkbaar met hetgeen bij een strekdam gebeurt: achter de dam ontstaat een luwtegebied, dat afhangt van de golflengte én de damlengte.
Kenmerkend voor diffractie is het “Fresnel-getal”:
(1) 
Waarin:
= de weglengteverschil [m] (zie figuur 1)
= de golflengte van het geluid [m]
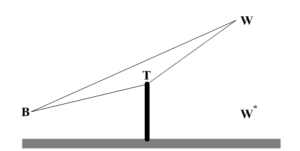
Nu kan zich een situatie voordoen als in figuur 2, waar een waarnemer over een obstakel heen vrij zicht heeft op de bron, met ander woorden zich niet in de schaduw van het obstakel bevindt. Toch kan diffractie aan het obstakel hier nog een rol spelen, zij het alleen bij kleine Nf.
figuur 2. waarnemer buiten de “schaduw” van een obstakel: = BW-BT-TW <0
Ingeval van figuur 2 wordt het weglengteverschil negatief genomen en krijgt dus ook Nf een negatieve waarde. Het geluidreducerend effect is maximaal voor δ→0 (zie tabel1) en de fysische interpretatie die we eraan moeten geven is dan ook dat de diffractie aan het obstakel een deel van de akoestische energie afbuigt, die in de ongestoorde situatie de waarnemer zou hebben bereikt. Anders gezegd: als diffractie een geluidniveau in de schaduwzone (W*) veroorzaakt, dan zal dientengevolge in W enige geluidreductie moeten optreden.
Met het Fresnel-getal wordt aan de hand van tabel 1 de reductie in geluidniveau per octaaf berekend ten opzichte van de situatie zonder obstakel. De tabel geldt voor een oneindig lang recht scherm en een lijnbron die daaraan parallel loopt.
| Fresnel-getal | reductie bij lijnbron 1 | reductie bij puntbron2 |
| Nf ≤ -0,3 | 0 | 0 |
| -0,3 ≤ Nf < 0 | 52⋅(Nf + 0,3)2 | 56⋅(Nf + 0,3)2 |
| 0 ≤ Nf < 1 | 4,68 + 5,4⋅√Nf | 5,04 + 8⋅√Nf |
| Nf ≥ 1 | 10,08 + 8⋅log Nf | 13,04 + 10⋅log Nf |
tabel 1. geluidreductie bij oneindig lang scherm (Maekawa)uitkomst van de formules is in dB of dB(A)
1 SRM-I hanteert alleen een grafische benadering
2 SRM-II hanteert een reeks machten van log(Nf)
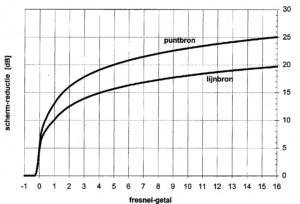
figuur 3. schermreductie volgens Maekawa
Voor eindig lange schermen al dan niet symmetrisch geplaatst, wordt verwezen naar de betreffende passages in het “Reken en Meetvoorschrift Verkeerslawaai” (module A025 Verkeerslawaai – basismodel wegverkeer). Overigens, het mag duidelijk zijn, dat de daarin opgenomen grafische bepaling van de schermwerking geen recht doet aan het frequentie-afhankelijke karakter daarvan, zoals het Fresnel-getal aangeeft. Hetzelfde bezwaar geldt trouwens voor de wijze waarop de lucht-, bodem- en meteo-demping in rekening worden gebracht volgens SRM-I (Standaard Reken Methode-I). Bij gebruik van SRM-I zal er daardoor (ten onrechte) geen verschil bestaan tussen het spectrum van de bron en dat van de waarnemer.
Literatuur
- Schermmodel volgens Maekawa