A025

Verkeerslawaai – basismodel wegverkeer

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Rekenmodel

Als basismodel kiezen we een zeer lange rechte weg, waarover zich een puntvormige bron beweegt, met een waarnemer op een afstand d loodrecht van de weg (figuur 1).

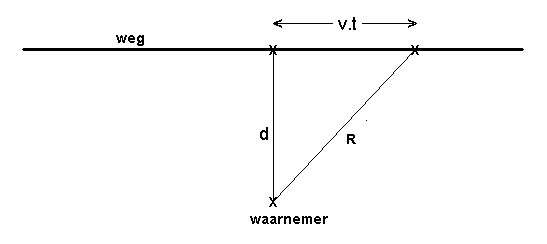
figuur 1. geluid van een bewegend voertuig dat wordt waargenomen

De afstand R tussen bron en waarnemer wordt beschreven door:

(1) $\begin{equation*} R =\sqrt{ d^2 + v^2 t^2} \end{equation*}$

Waarin:
d = de loodrechte afstand tot de weg [m]
v = de snelheid van de puntbron, i.c. een voertuig [m/s]
t = de tijd, met als nulpunt het moment van loodrechte passage [s]

Voor puntbronnen in een vrij veld kan de geluiddruk in het waarneempunt gerelateerd worden aan de geluiddruk op één meter van de puntbron:

(2) $\begin{equation*} p^2_{1m} \cdot \frac{1}{R^2} \end{equation*}$

Vooralsnog nemen we aan dat (2) geldig blijft bij A-gewogen geluiddrukken, en schrijven voor het equivalent geluidniveau ten gevolge van één bron:

(3) $\begin{equation*} L^{1}_{Aeq} = 10 \log \frac{1}{T} \int_{-T/2}^{T/2} \left( \frac{p^2_{A,1m}}{p^2_0} \frac{1}{d^2 + v^2 t^2} \right) dt \quad [\mathrm{dB(A)}] \end{equation*}$

Uitwerking van (3) geeft:

(4) $\begin{equation*} L_{Aeq}^1 = 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right + 10 \log \left( \frac{1}{T} \cdot \frac{2}{v \cdot d} \cdot \arctan\left \frac{vT}{2d} \right) \right \end{equation*}$

en met de aanname dat vT>d, zodat $\frac{vT}{2d}\approx \frac{\pi}{2}$ , volgt:

(5) $\begin{equation*} L_{Aeq}^1 = 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right + 10\log \left \frac{1}{T} \frac{\pi}{v \cdot d} \right \end{equation*}$

Stel nu dat er Q identieke voertuigen per seconde over de weg passeren, dan bedraagt het aantal bronnen over de middelingstijd dus QT; dit verhoogt het geluidniveau van (5) dus met 10log(QT).

Het totale equivalente niveau kan nu geschreven worden als:

(6) $\begin{equation*} L_{Aeq} = 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right + 10\log \left \frac{Q}{v} \frac{\pi}{d} \right \end{equation*}$

Gebruikelijk is om de verkeersintensiteit uit te drukken in het aantal voertuigen per uur en de snelheid in km/h; conversie van formule (6) in die zin geeft het equivalent geluidniveau bij een oneindig lange rechte weg (per voertuigcategorie !):

(7) $\begin{equation*} L_{Aeq} = 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right -30 + 10\log \left \frac{Q}{v} \right+ 10\log\left\frac{\pi}{d} \right \ [\mathrm{dB(A)}] \end{equation*}$

Waarin:
d = de loodrechte afstand van het waarneempunt tot de weg [m]
Q = het aantal passerende ‘identieke’ voertuigen per uur
v = de snelheid van de betreffende voertuigen [km/h]

Voor in werkelijkheid optredende situaties lijkt het basismodel alleszins bruikbaar als we de verkeersstroom opdelen in verschillende rijstroken en voertuigcategorieën met elk een bijbehorende gemiddelde snelheid en vervolgens (energetisch) sommeren. Deze aanpak is ook inderdaad terug te vinden in de standaard-rekenmethodes I en II.

Formule (7) geldt voor een oneindig lange rechte weg (en voldoende middelingstijd!). De vraag is of het model niet gemodificeerd kan worden voor meer realistische situaties. Stel: De weg is opgebouwd uit een aantal rechte wegsegmenten (zie figuur 2) en tevens wordt de integraal in formule (3) opgedeeld in een aantal tijdstappen, zodanig dat elke tijdstap correspondeert met het wegsegment dat de puntbron aflegt.

Voor de middelingstijd T geldt dus:

$T = \sum\limits_{j}(t_j - t_{j-1})$

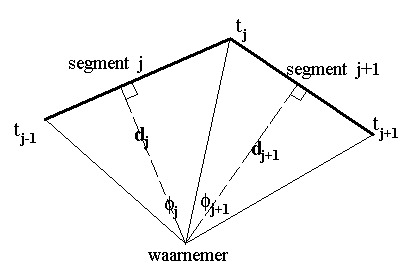
figuur 2. wegsegmentatie

Duiden we de loodrechte afstand tussen segment en waarnemer aan met d_j, de snelheid op dat segment met v_j en het moment van loodrechte passage met t_j⊥ , dan volgt voor een enkele puntbron:

(8) $\begin{equation*} \begin{algned} $L_{Aeq}^1 = 10 \log \left \frac{1}{T}\right\sum\limits_{j}\int_{t_{j-1}}^{t_j} \frac{p_{A,\text{1m}}^2}{p_0^2} \cdot \frac{1}{d_j^2 + v_j^2 (t - t_j\perp)^2} \, dt$ =\\ =10 \log \left \frac{p^2_{A,\text{1m}}}{p_0^2} \right + 10 \log \left [ \frac{1}{T} \sum\limits_{j}\frac{1}{v_j \cdot d_j} ( \arctan\left \frac{v_j (t_j - t_{j\perp})}{d_j} \right - \arctan\left\frac{v_j (t_{j-1} - t_{j\perp})}{d_j} \right] ) \end{aligned} \end{equation*}$

Vanuit het waarneempunt wordt een wegsegment gezien onder een zichthoek $\varphi_j$ volgens:

(9) $\begin{equation*} \varphi_j = \arctan \left \frac{v_j \cdot (t_j - t_{j\perp})}{d_j} - \arctan\left \frac{v_j \cdot (t_{j-1} - t_{j\perp})}{d_j} \end{equation*}$

zodat formule (6) geschreven kan worden als:

(10) $\begin{equation*} L_{Aeq}^1 = 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right + 10 \log \left \frac{1}{T} \sum\limits_{j}\frac{\varphi_j}{v_j \cdot d_j} \end{equation*}$

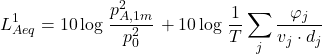
Op dezelfde wijze als bij de formule (6) brengen we de verkeersintensiteit Q in rekening en converteren we naar snelheden in km/h. Bij één enkele weg en normaal doorstromend verkeer mag de verkeersintensiteit bovendien overal constant verondersteld worden. Daarmee vinden we de volgende uitdrukking voor het equivalent geluidniveau bij een gesegmenteerde weg (per voertuigcategorie en per rijstrook !):

(11) $\begin{equation*} L_{Aeq}= 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right - 30 + 10 \log \left (Q \sum\limits_{j}\frac{\varphi_j}{v_j \cdot d_j}\right)[\mathrm{dB(A)}] \end{equation*}$

Waarin :
Q = het aantal over de weg, i.c. rijstrook passerende ‘identieke’ voertuigen [h^-1]
d_j = de loodrechte afstand tot de betreffende rijstrook van het j^ewegsegment [m]
= de zichthoek op j^ewegsegment [rad]
v_j = de snelheid op de betreffende rijstrook van het j^ewegsegment [km/h]

In feite stelt formule (8) de energetische sommatie voor over alle wegsegmenten. Zodra we te maken krijgen met samenvoeging van wegen (figuur 3), zal het totale geluidniveau gesommeerd moeten worden over alle verkeersstromen (=wegen); het segment waarop het verkeer samenstroomt, komt dan tweemaal voor: met verkeersintensiteit Q_weg1 respectievelijk Q_weg2. Dit komt erop neer dat zo’n segment eenmaal met intensiteit Q_weg1+Q_weg2 geteld wordt.

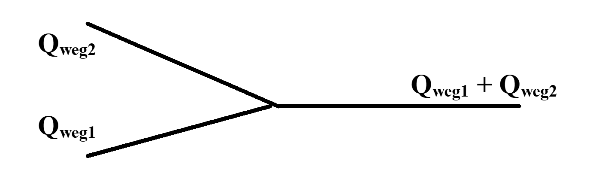
A black line with a white background AI-generated content may be incorrect.

figuur 3. sommatie van verkeersstromen

Met andere woorden: we kunnen ook de verkeersintensiteit per segment definiëren en komen zo tot een equivalent geluidniveau per wegsegment j:

(12) $\begin{equation*} L_{Aeq,j}= 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right - 30 + 10 \log \left \frac {Q_j}{v_j}\right + 10\log \left \frac {\varphi_j}{d_j}\right \mathrm{dB(A)}] \end{equation*}$

Eenvoudig is na te gaan dat bij een oneindig lange rechte weg een en ander overgaat in (7).Opdeling in segmenten (sectorverdeling) heeft wel plaats bij standaard-rekenmethode II, maar niet bij standaard-rekenmethode I.

Het voorgaande model beschrijft nog slechts de bronterm, de geometrische uitbreiding van het geluid en de wijze waarop wegdelen bijdragen aan het totale niveau. Op elk van die bijdragen dienen eerst nog correcties toegepast te worden in verband met overdrachtsdemping, reflectie, afscherming, type wegdek en helling; een en ander wordt nader uitgewerkt in de standaard-rekenmethodes I en II.

Formules (7) en (12) laten in ieder geval zien, dat de samenhang tussen geluidniveau en afstand tot de weg overeenkomt met die voor een lijnbron. De geometrische uitbreiding is in deze vorm aanwezig in de standaardrekenmethodes (SRM-I en -II). Lastiger is te doorzien hoe de bronterm (emissieterm) in beide methodes tot stand komt, althans hoe ogenschijnlijk verschillende methodieken tot dezelfde uitkomst kunnen leiden. Bij beide methoden worden emissiekentallen α en β per categorie voertuigen gehanteerd, die we hier ter onderscheiding voorzien van de index I respectievelijk II.

SRM-I sluit aan bij formule (7) en hanteert in feite de volgende benadering voor de emissie:

(13) $\begin{equation*} 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right - 30 + 10 \log \pi = \alpha_{\text{I}} + \beta_{\text{I}} \cdot v \end{equation*}$

Waarmee formule (5) geschreven kan worden als:

(14) $\begin{equation*} L_{Aeq} = \alpha_{\text{I}} + \beta_{\text{I}} \cdot v + 10 \log \left \frac{Q}{v}\right - 10\log {d} \end{equation*}$

De eerste drie termen in het rechterlid van formule (12; module “Constructiegeluid en trillingen”) vormen het emissiegetal E in SRM-I, dat dus overeenkomt met het equivalent geluidniveau op één meter afstand van de weg (L_Aeq,1m).

categorie	α_I	β_I
(1) motorrijwielen	62,7	0,19
(2) lichte voertuigen	51,2	0,21
(3) middelzware voertuigen	68,4	0,09
(4) zware voertuigen	76,2	0,03

tabel 1. emissie-kentallen SRM-I

SRM-II sluit aan bij formule (12), maar neemt het A-gewogen vermogensniveau van de puntbron als uitgangspunt en benadert dit vervolgens voor iedere octaafband met α en β:

(15) $\begin{equation*} 10 \log \left \frac{p_{A,1m}^2}{p_0^2} \right = L_{\text{W, Agewogen}} - 10\log {4\pi} = \alpha_{\text{II}} + \beta_{\text{II}} \cdot v - 10\log {4\pi} \end{equation*}$

waarmee formule (10) geschreven kan worden als:

(16) $\begin{equation*} L_{Aeq,j} = \alpha_{\text{II}} + \beta_{\text{II}} \cdot v + 10 \log \left \frac{Q_j}{v_j}\right + 10 \log \left \frac{\varphi_j}{d_j}\right - 41 \end{equation*}$

of als de zichthoek naar graden geconverteerd wordt:

(17) $\begin{equation*} L_{Aeq,j} = \alpha_{\text{II}} + \beta_{\text{II}} \cdot v + 10 \log \left \frac{Q_j}{v_j} \right + 10 \log \left \frac{\varphi_{\text{j, graden}}}{d_j} \right - 58.6 \end{equation*}$

De eerste drie termen in het rechterlid van formule (17) vinden we terug in SRM-II als de emissieterm L_E.

	motorrijwielen		lichte voertuigen		middelzware voertuigen		zware voertuigen
frequentie	α_II	β_II	α_II	β_II	α_II	β_II	α_II	β_II
63 Hz	77,2	0,10	69,2	0,07	94,1	-0,25	102,5	-0,32
125 Hz	81,8	0,19	73,6	0,18	91,8	0,01	99,9	-0,06
250 Hz	86,2	0,19	75,6	0,21	91,7	0,11	99,8	0,05
500 Hz	89,3	0,19	79,9	0,19	89,6	0,17	98,0	0,10
1000 Hz	91,5	0,19	81,8	0,20	99,0	0,07	106,9	0,01
2000 Hz	91,2	0,19	81,1	0,20	97,5	0,07	105,4	0,01
4000 Hz	86,7	0,19	79.0	0,18	89,8	0,12	97,7	0,06
8000 Hz	86,6	0,10	77,0	0,09	83,9	0,07	91,8	0,01

tabel 2. emissie-kentallen SRM-II

Formule (13) respectievelijk (15) tonen, dat de piekwaarde van de geluiddruk respectievelijk het bronvermogen, afhankelijk zijn gesteld van de voertuigsnelheid. Dit hangt samen met de lawaaiproductie van voertuigen, die naar herkomst onderscheiden wordt in:

motorgeluiden: aandrijfwerk, uitlaat, luchtaanzuiging, koeling;
rijgeluiden: banden, windgeruis, remmen, rammelen van carrosserie en lading.

In de term $\alpha+ \beta \cdot v$ zijn al deze stochastische aspecten verwerkt; ook de verschillen in rijstijl.

Standaard Rekenmethode-I en -II

De standaard rekenmethodes-I en -II worden volledig beschreven in het “Besluit Reken- en Meetvoorschrift Verkeerslawaai” (Wet Geluidhinder) van 22 mei 1981.

SRM-II onderscheidt zich van SRM-I op de volgende punten:

emissie gebaseerd op het akoestisch vermogen per octaafband (63Hz t/m 8kHz);
onderverdeling in sectoren;
per sector en per octaafband rekenen met lucht-, bodem- en meteo-demping,
schermwerking, reflecties, wegdektype, weghelling en kruispunttoeslag;
berekening van reflecties via “spiegeling” van bronpunten (≡rijlijnen);
berekening van schermwerking alsof sprake is van puntbronnen.

De hoofdformule voor SRM-II luidt dan ook:

(18) $\begin{equation*} L_{Aeq} = 10 \log \left \sum\limits_{i}\sum\limits_{j}\sum\limits_{n}\sum\limits_{m} 10^{L_{eq,i,j,n,m}/10} \right \text{ dB(A)} \end{equation*}$

Waarin L_eq,i,j,n,m de bijdrage is aan L_Aeq in één octaafband (i), van één sector (j), van één bronpunt (n) en van een voertuigcategorie (m). Deze term is als volgt opgebouwd:

(19) $\begin{equation*} L_{eq, i, j, n, m} = L_E + \Delta L_{KR} +\Delta L_{GU} - \Delta L_{OD} - \Delta L_{SW} - \Delta L_{R} - 58,6 \end{equation*}$

Waarin:
L_E = de emissieterm (zie ook formule 17), inclusief correctie voor wegdek en helling
ΔL_KR= de kruispunttoeslag (indien van toepassing)
ΔL_GU= de geometrische uitbreiding (zie formule 17)
ΔL_OD= de overdrachtsdemping (lucht, bodem en meteo-effecten)
ΔL_SW= de schermwerking (indien van toepassing)
ΔL_R= de invloed reflecties (indien van toepassing)

Het bovenstaande geeft al enigszins aan, dat SRM-II bepaald geen handmethodiek is. SRM-II mag ook slechts toegepast worden indien een prognose op basis van SRM-I ontoereikend is, dat wil zeggen: “naar het oordeel van de inspecteur voor de betreffende situatie niet tot een representatief equivalent geluidniveau leidt”. We beperken ons daarom in het navolgende tot SRM-I, waarvan de hoofdformule qua structuur overigens sterk lijkt op formule (19).

Auteurs

ir. L. Nederlof

prof.ir. J.J.M. Cauberg

Niveau

bachelor

master

Verkeerslawaai – basismodel wegverkeer

Rekenmodel

Standaard Rekenmethode-I en -II

Auteurs

Niveau

Tags

Onze partners

Over Klimapedia