B005

Warmtetransport door straling

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Warmtetransport, algemeen

In de brandveiligheid worden, net als in de overige bouwfysische vakgebieden, drie principiële warmtetransportmechanismen onderscheiden:

geleiding
convectie (stroming)
straling

Ad 1: geleiding

Geleiding treedt op bij warmtetransport door vaste materialen. Hoewel dit transport in theorie ook optreedt in vloeistoffen en gassen, is het hier meestal volledig ondergeschikt aan het stromingstransport. Het warmtetransport door geleiding in het materiaal komt tot stand onder invloed van een temperatuurverschil over het materiaal, waarbij de mate van geleiding wordt bepaald door de warmtegeleidingscoëfficient van het materiaal.

Ad 2: convectie

Convectie of stromingstransport treedt op in vloeistoffen en gassen. De warmte-inhoud van het materiaal wordt door het massatransport verplaatst. Dit stromingstransport komt tot stand door een drukverschil. Dit drukverschil wordt overigens, in geval van brand, vaak door een temperatuurverschil veroorzaakt.

Ad 3: straling

Stralingsoverdracht komt niet via een materiaal tot stand, maar is het gevolg van emissie van infrarode (elektromagnetische) straling aan het materiaaloppervlak. Dit kan een vast materiaal zijn, maar ook een vloeibaar of gasvormig materiaallichaam, zoals een vlam.

Warmtetransport door straling

Warmtetransport door straling bestaat uit energietransport door elektromagnetische golven. Het gaat om een relatief klein deel van het elektromagnetische spectrum, variërend van zichtbaar licht tot diep infrarood; dit komt overeen met golflengten tussen λ = 0,4 en 100 μm. Voor dit warmtetransport is geen transportmedium noodzakelijk, het komt dus ook in een vacuüm voor.

Stralingsoverdracht is vooral belangrijk bij hoge temperaturen (vanaf circa 400 ^oC); bij lagere temperaturen overheerst het convectieve warmtetransport. Bij een temperatuur van het stralingsvlak van 550 ^oC wordt ook in het zichtbare gebied zoveel straling geëmitteerd dat dit waarneembaar is als een rode gloed. Bij een verdere temperatuurverhoging verandert de kleur van het stralende vlak (zie tabel 1).

temperatuur [^oC]	kleur
550	juist zichtbare rode gloed
700	vol rood
900	kersenrood
1100	oranje
1400	wit

tabel 1. zichtbare kleur van hittestralende objecten

De kleurverandering is het gevolg van de verandering van het spectrum van de emissie. Voor een ideale emittor (zwarte straler) is de “quantumtheorie van Planck” geldig, waarin de elektromagnetische straling discontinu, in discrete hoeveelheden (quanta) wordt uitgezonden:

(1) $\begin{equation*} E_{b,\lambda} = \frac{2 \pi c^2 h \lambda^{-5}}{\exp\left( \frac{ch}{\lambda k T} \right) - 1} \; [\mathrm{W/m^{2}\cdot \mu m}] \end{equation*}$

Waarin:
E_b,λ = het totale vermogen, uitgezonden per oppervlakte-eenheid door een zwarte straler in een smalle golflengteband (tussen λ en λ+dλ).
λ = de golflengte [μm]
c = de snelheid van het licht
h = de constante van Planck
k = de constante van Boltzmann
T = de absolute temperatuur [K]

De maximale stralingsvermogensdichtheid wordt bereikt bij een kortere golflengte, naarmate de temperatuur toeneemt, zoals beschreven in de “wet van Wien”:

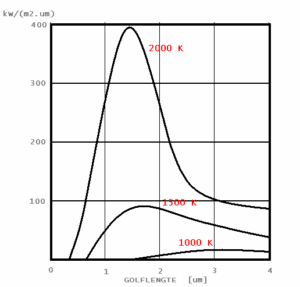
(2) $\begin{equation*} \lambda_\text{max} T = 2,9 \cdot 10^3 \; [\mathrm{ \mu m \cdot K }] \end{equation*}$

Zo bevindt zich het maximum bij een temperatuur van 1000 K, bij een golflengte van λ_max= 2,9 μm. Bij 2000 K is dit λ_max= 1,45 μm (zie figuur 1).

figuur 1. emissie van een zwarte straler als functie van golflengte en temperatuur

Het emissievermogen over het hele spectrum van een zwarte straler wordt verkregen door integratie van vergelijking (1) tussen de golflengten λ = 0 en λ = ∞ :

(3) $\begin{equation*} E_b = \int_0^{\infty} E_{b,\lambda} \cdot\, d\lambda = \frac{2 \pi^5 k^4 T^4}{15 c^2 h^3} \; [\mathrm{W/m^{2}}] \end{equation*}$

De werkelijke emissie zal in het algemeen lager zijn dan die van een zwarte straler. Dit wordt weergegeven met de emissiecoëfficient ε, die golflengte-afhankelijk kan zijn:

(4) $\begin{equation*} \varepsilon = \frac{E_\lambda}{E_{b,\lambda}} \end{equation*}$

Hierin in E_λ de stralingsvermogensdichtheid van het werkelijk oppervlak tussen λ en λ+dλ. Vergelijking (3) gaat daarmee, bij een perfect absorberend lichaam (α=1, en daarmee ook ε=1) over in:

(5) $\begin{equation*} E = \varepsilon \sigma T^4 \; [\mathrm{W/m^{2}}] \end{equation*}$

De grootheid σ wordt de “constante van Stefan-Boltzmann” genoemd:

(6) $\begin{equation*} \sigma = \frac{2 \pi^5 k^4}{15 c^2 h^3} = 5,67 \cdot 10^{-8} [\mathrm{W/(m^{2}K^4)}] \end{equation*}$

Voor twee evenwijdige, oneindig grote vlakken, met temperaturen T₁ van het stralende vlak en T₂ van het ontvangende vlak, en bijbehorende emissiefactoren ε₁ en ε₂ gaat vergelijking (5) over in:

(7) $\begin{equation*} E= \varepsilon_\text{res} \sigma (T_1^4 - T_2^4) [\mathrm{W/m^{2}}] \end{equation*}$

Hierin is:

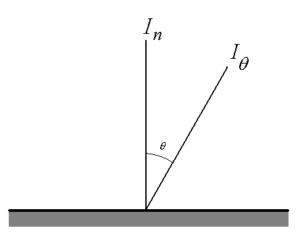
$\frac{1}{\varepsilon_\text{res}} =\frac{1}{\varepsilon_1} + \frac{1}{\varepsilon_2} - 1$

De oppervlakte van een stralend vlak zendt warmtestraling uit in diverse richtingen. Wanneer de stralingsintensiteit loodrecht op het oppervlak I_n bedraagt, dan is de intensiteit in de richting θ gelijk aan:

(8) $\begin{equation*} I_\theta = I_n \cos \theta \end{equation*}$

figuur 2. stralingsintensiteit in diverse richtingen vanuit het oppervlak

Geïntegreerd over de halve ruimtehoek (de totale zichthoek vanaf de oppervlakte van het vlak is de binnenzijde van een halve bol), geldt voor de totale emissievermogensdichtheid:

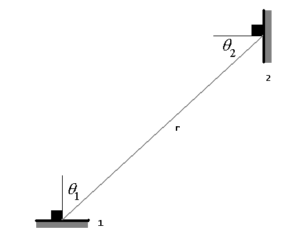
(9) $\begin{equation*} E = \pi I_n \; [\mathrm{ W / m^2 }] \end{equation*}$

Bij de stralingsuitwisseling tussen twee willekeurig georiënteerde vlakjes gaat het doorgaans slechts om een relatief kleine ruimtehoek. Voor de stralingsuitwisseling tussen de twee vlakjes kan worden geschreven (van vlakje 1 naar vlakje 2):

$q = E \cdot \int_0^{A_1} \frac{\cos \theta_1 \cos \theta_2}{\pi r^2} \cdot d A_1$

(10) $\begin{equation*} q = \phi E \; [\mathrm{ W / m^2 }] \end{equation*}$

Hierin is Φ de zicht- of blikfactor. Figuur 3 geeft dit schematisch weer.

figuur 3. stralingsuitwisseling, afhankelijk van de zichtfactor

Het bepalen van de zichtfactor is gecompliceerd. Vanuit een klein vlakje dA gezien is de zichtfactor dat gedeelte van de halve bol dat door de projectie van het stralende vlak wordt belemmerd. Feitelijk is dit het eenvoudigst te bepalen met behulp van bolcoördinaten in plaats van carthesische coördinaten.

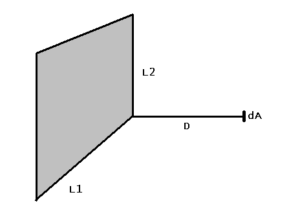
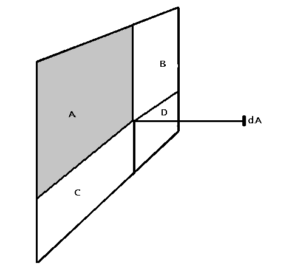
Uiteraard zijn hiervoor diverse hulpmiddelen ontwikkeld. Tabel 2 vormt een dergelijk hulpmiddel. Hiermee is het mogelijk om in een willekeurig punt, gelegen in een vlak op een vaste afstand van het warmtestralend vlak de blikfactor te bepalen. Bij de tabel hoort figuur 4. Het totale stralende vlak bestaat uit 4 van deze deelvlakken (kwadranten), zie figuur 5. Door sommatie van de 4 bijbehorende zichtfactoren uit tabel 2 wordt de totale zichtfactor bepaald.

figuur 4. ontvangvlakje dA op de normaal vanuit een hoekpunt van het stralend vlak L1xL2 (zie tabel 2 voor de zichtfactoren)

α	S=1	S=0,9	S=0,8	S=0,7	S=0,6	S=0,5	S=0,4	S=0,3	S=0,2	S=0,1
10,0	0,231	0,231	0,231	0,230	0,228	0,226	0,222	0,215	0,204	0,177
5,0	0,215	0,215	0,214	0,213	0,211	0,207	0,201	0,190	0,176	0,144
4,0	0,208	0,208	0,207	0,205	0,203	0,199	0,193	0,181	0,166	0,133
3,0	0,197	0,197	0,196	0,194	0,191	0,186	0,180	0,168	0,152	0,120
2,0	0,178	0,178	0,177	0,175	0,172	0,167	0,161	0,149	0,132	0,102
1,0	0,139	0,138	0,137	0,136	0,133	0,129	0,123	0,113	0,099	0,075
0,9	0,132	0,132	0,131	0,130	0,127	0,123	0,117	0,108	0,094	0,075
0,8	0,125	0,125	0,124	0,122	0,120	0,116	0,111	0,102	0,089	0,067
0,7	0,117	0,116	0,116	0,115	0,112	0,109	0,104	0,096	0,083	0,063
0,6	0,107	0,107	0,106	0,105	0,103	0,100	0,096	0,088	0,077	0,058
0,5	0,097	0,096	0,096	0,095	0,093	0,090	0,086	0,080	0,070	0,053
0,4	0,084	0,083	0,083	0,082	0,081	0,079	0,075	0,070	0,062	0,048
0,3	0,069	0,068	0,068	0,068	0,067	0,065	0,063	0,059	0,052	0,040
0,2	0,051	0,051	0,050	0,050	0,049	0,048	0,047	0,045	0,040	0,032
0,1	0,028	0,028	0,028	0,028	0,028	0,028	0,027	0,026	0,024	0,021
0,09	0,026	0,026	0,026	0,026	0,025	0,025	0,025	0,024	0,022	0,019
0,08	0,023	0,023	0,023	0,023	0,023	0,023	0,022	0,022	0,020	0,017
0,07	0,021	0,021	0,021	0,021	0,020	0,020	0,020	0,019	0,018	0,016
0,06	0,018	0,018	0,018	0,018	0,018	0,017	0,017	0,017	0,016	0,014
0,05	0,015	0,015	0,015	0,015	0,015	0,015	0,015	0,014	0,014	0,013
0,04	0,012	0,012	0,012	0,012	0,012	0,012	0,012	0,012	0,011	0,010
0,03	0,009	0,009	0,009	0,009	0,009	0,009	0,009	0,009	0,009	0,008
0,02	0,006	0,006	0,006	0,006	0,006	0,006	0,006	0,006	0,006	0,006
0,01	0,003	0,003	0,003	0,003	0,003	0,003	0,003	0,003	0,003	0,003

tabel 2. waarden van de zichtfactor Φ voor verschillende waarden van α en S

Hierin is:
$a = (L_1 \cdot L_2 ) / D^2$
$S = L_2 / L_1$

Het totale gevelvlak bestaat uit vier kwadranten (zie figuur 5). De totale zichtfactor wordt simpelweg verkregen door de zichtfactoren van de vier kwadranten bij elkaar op te tellen:

(11) $\begin{equation*} \phi_{\text{totaal}} = \phi_A + \phi_B + \phi_C + \phi_D \end{equation*}$

figuur 5. de totale warmtestraling in dA bestaat uit de som van de warmtestraling vanuit de vier verschillende kwadranten

Voorbeeld: scheidingswand van een brandcompartiment

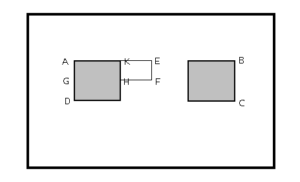
De gevelconstructie van figuur 6 is brandwerend uitgevoerd, met uitzondering van de twee daglichtopeningen. Op een afstand van 5 meter bevindt zich een tegenover liggende gevel. Is dit mogelijk zonder aanvullende voorzieningen aan de daglichtopeningen te treffen?

figuur 6. voorbeeld gevelconstructie

Gegeven
De raamopeningen zijn 1,0 x 1,0 m² groot, met een onderlinge afstand van 1,5 m. het totale gevelvlak is 5 x 3 m groot. De bronstraling vanuit de raamopeningen bedraagt 100 kW/m². Als grenswaarde voor de ontvangende warmtestralingsflux geldt 15 kW/m².

Antwoord
Het gaat erom de maximale warmtestralingsflux te toetsen aan de gegeven grenswaarde. De maximale warmtestralingsflux op het tegenovergelegen gevelvlak zal zich midden tussen de twee raamopeningen bevinden. Dit houdt in dat alleen het vlak ABCD beschouwd hoeft te worden.

Uit symmetrie-oogpunt kan worden gesteld:

$\phi_{\text{ABCD}} = 4 \cdot \phi_{\text{AKHG}} = 4 \cdot (\phi_{\text{AEFG}} - \phi_{\text{KEFH}})$

Uit tabel 2 volgt:
S_AEFG = 0,50 / 1,75 = 0,28; α_AEFG = (1,75 x 0,50) / (5,0)² = 0,035; Φ =0,0104
S_KEFH = 0,50 / 0,75 = 0,67; α_KEFH = (0,75 x 0,50) / (5,0)² = 0,015; Φ =0,0045

Dus:
Φ = 4 x (0,0104 – 0,0045) = 0,0236.

Bij een bronstraling van 100 kW/m² is de ontvangende straling 2,36 kW/m². Deze overschrijdt de grenswaarde van 15 kW/m² niet, zodat geen brandwerende voorzieningen noodzakelijk zijn.

stralingsflux [kW/m²]	omschrijving
0,7	zonnestraling op een zomerdag op 52^o NB.
1,0	grenswaarde voor (langdurige) blootstelling van de huid zonder schadelijke gevolgen
6,4	pijn na 8 s blootstelling van de huid
10,4	pijn na 3 s blootstelling van de huid
16	verbranding van de huid na 5 s
29	spontane ontbranding van hout bij langdurige blootstelling

tabel 3. warmtestraling, enkele kenmerkende waarden

Auteurs

ir. R.A.P. van Herpen

Warmtetransport door straling

Warmtetransport, algemeen

Ad 1: geleiding

Ad 2: convectie

Ad 3: straling

Warmtetransport door straling

Voorbeeld: scheidingswand van een brandcompartiment

Auteurs

Tags

Onze partners

Over Klimapedia