B003

Warmtetransport door geleiding

Bekijk de transponeringstabel om te zien welke wetsartikelen uit het BB overeenkomen met die uit het BBL.

Warmtetransport, algemeen

In de brandveiligheid worden, net als in de overige bouwfysische vakgebieden, drie principiële warmtetransportmechanismen:

geleiding
convectie (stroming)
straling

Ad 1: geleiding

Geleiding treedt op bij warmtetransport door vaste materialen. Hoewel dit transport in theorie ook optreedt in vloeistoffen en gassen, is het hier meestal volledig ondergeschikt aan het stromingstransport. Het warmtetransport door geleiding in het materiaal komt tot stand onder invloed van een temperatuurverschil over het materiaal, waarbij de mate van geleiding wordt bepaald door de warmtegeleidingscoëfficient van het materiaal.

Ad 2: convectie

Convectie of stromingstransport treedt op in vloeistoffen en gassen. De warmte-inhoud van het materiaal wordt door het massatransport verplaatst. Dit stromingstransport komt tot stand door een drukverschil. Dit drukverschil wordt overigens, in geval van brand, vaak door een temperatuurverschil veroorzaakt.

Ad 3: straling

Stralingsoverdracht komt niet via een materiaal tot stand, maar is het gevolg van emissie van infrarode (elektromagnetische) straling aan het materiaaloppervlak. Dit kan een vast materiaal zijn, maar ook een vloeibaar of gasvormig materiaallichaam, zoals een vlam.

Stationair warmtetransport door geleiding

Eendimensionaal warmtetransport door een materiaal als gevolg van geleiding kan als volgt worden beschreven:

(1) $\begin{equation*} q=-\lambda \cdot \frac{dT}{dx} \end{equation*}$

Dit geeft:

(2) $\begin{equation*} q \cdot \int_{0}^{L} dx = -\lambda \cdot\int_{T2}^{T1} dT \end{equation*}$

Ervan uitgaande dat de warmtegeleidingscoëfficient λ onafhankelijk is van de temperatuur van het materiaal, kan dit worden uitgewerkt tot:

(3) $\begin{equation*} q =\frac{\lambda}{L} (T_1 - T_2) \end{equation*}$

Waarin:
$q$ = de warmtestroomdichtheid [W/m²]
$\lambda$ = de warmtegeleidingscoëfficient [W/(m.K)]
T = de temperatuur [K]
x = de afstand [m]

Figuur 1 geeft deze relatie schematisch weer.

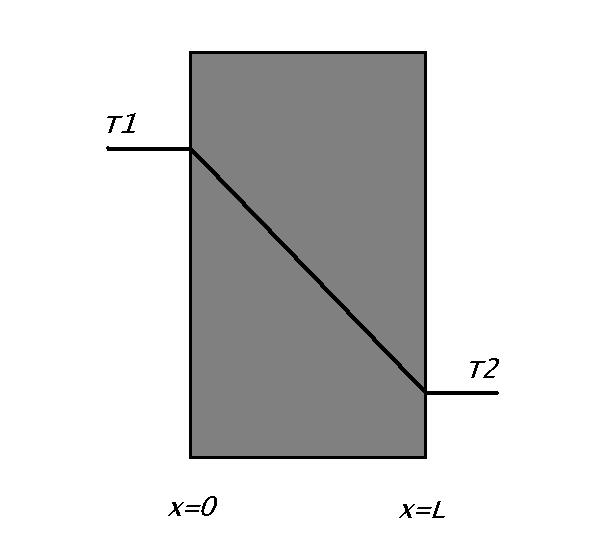
figuur 1. temperatuurverloop bij ééndimensionaal warmtetransport door geleiding

Bij samengestelde constructies, bestaande uit meer dan één materiaallaag, gaat de gegeven relatie voor elke materiaallaag afzonderlijk op. In figuur 2 is dit weergegeven.

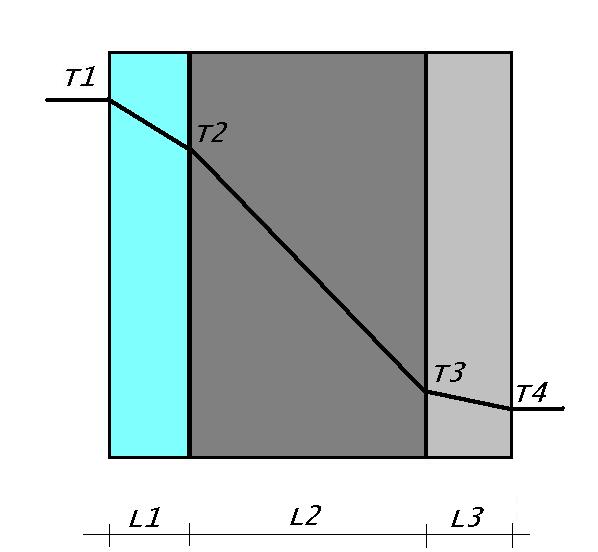
figuur 2. temperatuurverloop bij ééndimensionaal warmtetransport door geleiding, meerlaagse constructie.

De warmtestroomdichtheid, behorende bij de doorsnede van figuur 2, bedraagt:

(4) $\begin{equation*} q=\frac{\lambda_1}{L_1} \cdot (T_1 - T_2) = \frac{\lambda_2}{L_2} \cdot (T_2 - T_3) = \frac{\lambda_3}{L_3} \cdot (T_3 - T_4) \end{equation*}$

Dit kan ook geschreven worden als:

(5) $\begin{equation*} q = \frac{T_1 - T_4}{(\frac{L_1}{\lambda_1}+\frac{L_2}{\lambda_2} +\frac{L_3}{\lambda_3})} \end{equation*}$

De term in de noemer van de bovenbeschreven vergelijking wordt wel de “warmteweerstand van de constructie” genoemd. Wanneer T₁ en T₄ in de doorsnede van figuur 2 luchttemperaturen zijn (in plaats van oppervlaktetemperaturen, zoals in figuur 2 is aangegeven), dient de warmteweerstand te worden vergroot met de overgangsweerstanden aan weerszijden van de constructie. De totale warmteweerstand bestaat dus uit de drie warmteweerstanden van de verschillende materiaallagen (L_i/λ_i), vermeerderd met de twee overgangsweerstanden.

Voorbeeld: scheidingswand van een brandcompartiment

De drielaagse constructie van figuur 2 heeft de volgende opbouw:

steenwol: λ=0,04 W/(m.K), L=0,06 m
beton: λ=2,0 W/(m.K), L=0,20 m
steenwol: λ=0,04 W/(m.K), L=0,06 m

Aan beide zijden van de constructie is een overgangscoëfficient aanwezig van h=25 W/(m²K), ofwel een overgangsweerstand van R=0,04 m²K/W

Vragen

Wat is de warmteweerstand van de constructie en wat is de totale warmteweerstand?
Wat is de maximale temperatuur in het beton, wanneer voor de temperatuur in de brandruimte 800 ^oC aangehouden kan worden, en in de aangrenzende ruimte 20 ^oC?

Antwoorden

De warmteweerstand van steenwol bedraagt: L / λ = 0,06 / 0,04 = 1,50 m²K/W. Voor beton is dit 0,20 / 2,0 = 0,10 m²K/W. De warmteweerstand van de constructie wordt daarmee: 1,50 + 0,10 + 1,50 = 3,10 m²K/W. rekening houdend met de overgangsweerstanden aan weerszijden van de constructie wordt de totale warmteweerstand 3,18 m²K/W.
De maximale temperatuur in het beton treedt in de stationaire situatie op op het scheidingsvlak tussen beton en steenwol, aan de zijde van de brandruimte. Aangezien het temperatuurverval in de constructie evenredig is met de warmteweerstand van de constructie kan geschreven worden:
T_max = 800 – (1,54 / 3,18) x (800 – 20) = 800 – 378 = 422 ^oC.
Aan de andere zijde van de materiaallaag beton bedraagt de temperatuur:
T_min = 20 + (1,54 / 3,18) x (800 – 20) = 20 + 378 = 398 ^oC.

Niet-stationair warmtetransport door geleiding

In brandsituaties is het stationair warmtetransport feitelijk niet zo interessant. Het kenmerk van brand is juist dat de temperatuur in de brandruimte snel erg hoog kan worden. Niet-stationair warmtetransport door de constructie leidt derhalve tot veel realistischer resultaten. Immers, door warmte- (of koude-) accumulatie in de constructie reageert de constructie traag. Deze thermische traagheid leidt tot minder extreme temperaturen in de constructie enerzijds, en een tijdsverschuiving voor de maximaal optredende temperatuur anderzijds.

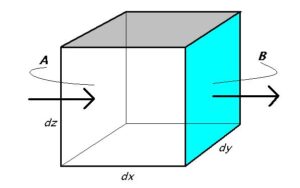
Het effect van de thermische traagheid wordt in de onderstaande relaties en de bijbehorende figuur 3 geïllustreerd. Daarbij wordt weer uitgegaan van warmtetransport in één richting (ééndimensionaal):

$q_x \cdot dS = -\lambda (\frac{\partial T}{\partial x}) dydz$

(6) $\begin{equation*} q_{x+dx} \cdot dS = -\lambda \left (\frac{\partial T}{\partial x} + \frac{\partial^2 T}{\partial x^2} dx \right ) dydz \end{equation*}$

figuur 3. warmtetransport (geleiding) door een volume-element van kleine afmetingen

Het verschil tussen de vergelijkingen aan het inkomende en het uitgaande oppervlak van het volume-element, moet worden goedgemaakt door de warmte-accumulatie enerzijds en een eventueel aanwezig warmtebron anderzijds. Dit leidt tot de volgende vergelijking:

(7) $\begin{equation*} \lambda \left \frac{\partial^2 T}{\partial x^2} dxdydz = \rho c \frac{\partial c}{\partial t} dxdydz - Qdxdydz \end{equation*}$

Hierin is $Q$ het vermogen dat per volume-eenheid wordt afgegeven. $\rho$ en c zijn respectievelijk de dichtheid en de warmtecapaciteit van het materiaal.

Dit kan worden vereenvoudigd tot:

(8) $\begin{equation*} \frac{\partial^2 T}{\partial x^2} = \frac{1}{\alpha} \cdot \frac{\partial T}{\partial t} - \frac{Q}{\lambda} \end{equation*}$

Hierin is α de “thermische diffusiteit” (of temperatuurvereffeningscoëfficiënt) van het materiaal $( \alpha = \lambda / (\rho c))$ . Deze grootheid wordt in de bovenstaande relatie constant verondersteld. In de meeste gevallen zal in het volume-element geen warmtebron aanwezig zijn. De grootheid $Q$ is dan 0. De vergelijking kan dan verder worden vereenvoudigd (eendimensionaal):

(9) $\begin{equation*} \frac{\partial^2 T}{\partial x^2} = \frac{1}{\alpha} \cdot \frac{\partial T}{\partial t} \end{equation*}$

Uitgebreid naar drie dimensies wordt dit:

(10) $\begin{equation*} \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} = \nabla^2 T = \frac{1}{\alpha} \cdot \frac{\partial T}{\partial t} \end{equation*}$

Bij een half-oneindig medium, welke aan het oppervlak wordt verhit, speelt de thermische diffusiteit samen met het tijdsinterval een rol in de bepaling van de meewerkende dikte van het materiaal. Dit is van belang om te kunnen bepalen of een materiaallaag in een niet-stationaire berekening als half-oneindig medium. Dit blijkt het geval te zijn wanneer wordt voldaan aan:

(11) $\begin{equation*} L > 2 \cdot \sqrt{\alpha \cdot t} \end{equation*}$

De grootheid $\sqrt{\alpha \cdot t}$ is de “karakteristieke thermische geleidingsdiepte” (of karakteristieke thermische indringingsdiepte) van het materiaal. Wanneer het materiaal meer dan tweemaal zo dik is als de karakteristieke thermische geleidingsdiepte kan het worden beschouwd als thermisch dik. Is dit niet het geval, dan is het materiaal thermisch dun.

Een andere, hiermee verband houdende grootheid is de thermische traagheid, meestal aangeduid met b. De thermische traagheid ligt als volgt vast:

(12) $\begin{equation*} b =\sqrt{\lambda \cdot \rho \cdot c} \end{equation*}$

Tabel 1 geeft van enkele veel voorkomende materialen de thermische diffusiteit en de thermische traagheid weer.

materiaal	eigenschappen (grootheden)
	λ	c_p	ρ	α	λ ρ c_p
	[W/m.K]	[J/kg.K]	[kg/m³]	[m²/s]	[W².s/m⁴K²]
koper	387,000	380	8940,0	1,14E-04	1,31E+09
staal	45,800	460	7850,0	1,27E-05	1,65E+08
metselwerk	0,690	840	1600,0	5,13E-07	9,27E+05
beton	2,000	880	2300,0	9,88E-07	4,05E+06
floatglas	0,760	840	2700,0	3,35E-07	1,72E+06
gipspleister	0,480	840	1440,0	3,97E-07	5,81E+05
PMMA	0,190	1420	1190,0	1,12E-07	3,21E+05
hardhout, eiken	0,170	2380	800,0	8,93E-08	3,24E+05
naaldhout, vuren	0,140	2850	640,0	7,68E-08	2,55E+05
asbest	0,150	1050	577,0	2,48E-07	9,09E+04
PUR-schuim	0,034	1400	20,0	1,21E-06	9,52E+02
lucht	0,026	1040	1,1	2,27E-05	2,97E+01

tabel 1. thermische eigenschappen van enkele veel voorkomende materialen

Voorbeeld: betonwand van een brandcompartiment

Kan een betonwand van 200 mm dikte gedurende het eerste kwartier van een brand als thermisch dik of thermisch dun worden beschouwd?

Antwoord

De karakteristieke thermische geleidingsdiepte bedraagt (zie tabel 1): 0,03 [m].

Zodra de dikte de grenswaarde van 60 mm overschrijdt kan het materiaal dus als thermisch dik worden beschouwd. Dat is hier het geval.

Wanneer de scheidingsconstructie geen enkelvoudige, massieve constructie is, maar uit verschillende materiaallagen is opgebouwd, moet voor de thermische traagheid b het volgende worden aangehouden:

indien de grootheid b van het niet-direct blootgestelde materiaal (2) groter is dan die van het direct blootgestelde materiaal (1), dus: b₂> b₁, geldt voor de samengestelde constructie: b = b₁.
in het andere geval, dus: b₂< b₁, hangt de grootheid b samen met de navolgende thermische geleidingsdiepte van materiaal (1):

$S_\text{1, lim}=\sqrt{\alpha \cdot t_d}$

Hierin in t_d de brandduur tot aan het begin van de doofperiode.

De thermische traagheid volgt nu uit:

Indien $S_1 > S_{1,\text{lim}}$ : $b = b_1$ ;
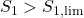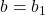Indien $S_1 < S_{1,\text{lim}}$ : $b = \frac{S_1}{S_{1,\text{lim}}} b_1 + \left( 1 - \frac{S_1}{S_{1,\text{lim}}} \right) b_2$

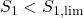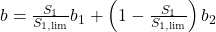
De thermische eigenschappen van veel bouwmaterialen zijn afhankelijk van de temperatuur van het materiaal. Meestal wordt temperatuur-onafhankelijkheid verondersteld (zie tabel 1). Tabel 2 geeft in dit verband beter op de praktijk aansluitende waarden voor enkele veel voorkomende bouwmaterialen.

materiaal	eigenschappen (grootheden)
	θ	λ	c_p	ρ	λ ρ c_p
	[°C]	[W/m.K]	[J/kg.K]	[kg/m³]	[W².s/m⁴K²]
grindbeton	20	2,000	900	2300,0	4,14E+06
	200	1,630	1020	2300,0	3,82E+06
	500	1,210	1165	2300,0	3,24E+06
	1000	0,830	1290	2300,0	2,46E+06
lichtbeton	20	1,000	840	1500,0	1,26E+06
	200	0,875	840	1500,0	1,10E+06
	500	0,688	840	1500,0	8,67E+05
	1000	0,500	840	1500,0	6,30E+05
staal	20	54,000	425	7850,0	1,80E+08
	200	47,000	530	7850,0	1,96E+08
	500	37,000	666	7850,0	1,93E+08
	1000	27,000	650	7850,0	1,38E+08
calcium-silicaatplaten	20	0,069	750	450,0	2,33E+04
	250	0,079	955	450,0	3,40E+04
	450	0,095	1060	450,0	4,53E+04
	1050	0,157	1440	450,0	1,02E+05
hout	20	0,170	1110	450,0	8,49E+04
	250	0,170	1125	450,0	8,61E+04
	450	0,170	1135	450,0	8,68E+04
	1050	0,170	1165	450,0	8,91E+04
metselwerk	20	1,000	1110	1800,0	2,00E+06
	200	1,020	1125	1800,0	2,07E+06
	500	1,180	1135	1800,0	2,41E+06
	1000	1,400	1165	1800,0	2,94E+06
glas	20	0,780	840	2700,0	1,77E+06

tabel 2. thermische eigenschappen van enkele bouwmaterialen, afhankelijk van de temperatuur

Auteurs

ir. R.A.P. van Herpen