Het verbrandingsproces

Verbranding is oxidatie van een stof, bij hoge temperatuur, waarbij warmte vrijkomt. Het is dus een exotherme reactie. Voor verbranding zijn brandstof en zuurstof nodig. Onder invloed van een ontstekingstemperatuur wordt de verbranding in gang gezet. Vervolgens onderhoud dit proces zichzelf; de energie die bij verbranding vrijkomt is groter dan de ontstekingsenergie. Daarbij worden verbrandingsproducten (geoxideerde producten) gevormd.

Wanneer de verbranding volledig plaatsvindt in een (denkbeeldig) volume dat wordt begrensd door een controlevlak, waarbij ter plaatse van het controlevlak de omgevingscondities gelden, spreekt men van een adiabatische verbranding.

Eerste hoofdwet voor een adiabatische stochiometrische verbranding

Beschouwen we eerst een adiabatische verbrandingskamer waarin een brandstof verbrand wordt zonder overmaat van lucht zoals aangeduid op onderstaande figuur:

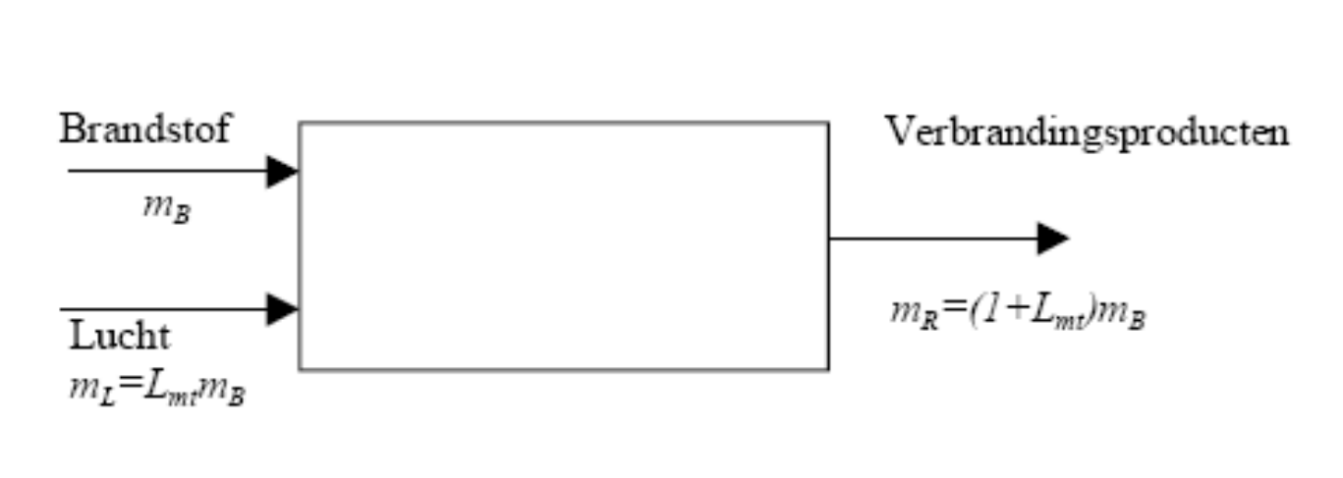
Voor het uitschrijven van de eerste hoofdwet maken we gebruik van de enthalpie van elke stofsoort (H), deze is samengesteld uit twee componenten: de vormingsenthalpie hf (die de relatie legt tussen de verschillende stofsoorten) en de enthalpie h die gerefereerd wordt naar de gekozen referentietoestand voor de vormingsenthapie. Omdat de meeste dat voor verbrandingsprocessen zich baseren op een referentietoestand met t=25°C en p=1 atm zullen we in wat volgt ook deze waarden gebruiken.

De eerste hoofdwet luidt nu:

of

of rekening houdend met het feit dat het verschil in vormingsenthalpieën gelijk is aan de verbrandingswaarde, met name:

(1)  

wordt de eerste hoofdwet voor de verbranding:

Dit wil zeggen dat we de verbranding in eerste instantie kunnen beschouwen als een proces waarbij een zekere hoeveelheid warmte wordt toegevoegd aan het systeem per kg toegevoerde brandstof.

Eerste hoofdwet-analyse voor een adiabatische verbranding met grote luchtovermaat

We kunnen een analoge redenering opbouwen voor een verbrandingsproces met ruime overmaat aan lucht. De overmaat aan lucht wordt hierbij aangegeven door de luchtfactor λ die de verhouding weergeeft tussen de effectieve hoeveelheid lucht die toegevoegd wordt t.o.v. de minimaal theoretisch vereiste luchthoeveelheid. De situatie wordt weergegeven in onderstaande figuur.

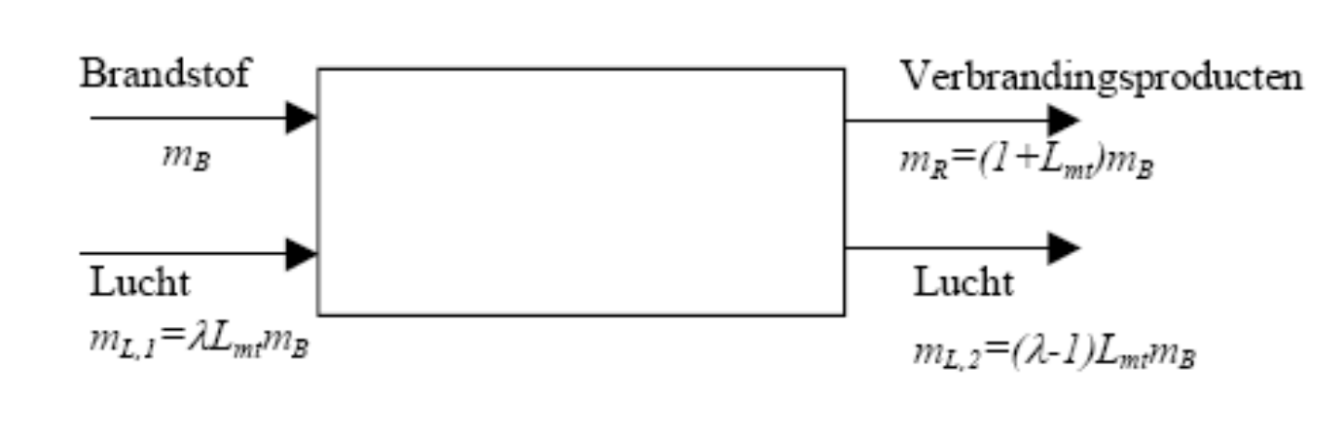
De eerste hoofdwet wordt nu:

of rekening houdend met (1):

De resterende termen die vormingsenthalpieën bevatten, vallen nu precies tegen elkaar weg. Indien λ nu zeer groot is, kan de vorige vergelijking benaderd worden met:

of

Deze benadering, die geldig is indien we met een grote overmaat aan lucht werken, kan geïnterpreteerd worden alsof de brandstof een zeker hoeveelheid warmte (gekoppeld aan zijn enthalpie) in het systeem brengt ter waarde van de verbrandingswaarde.

Tweede hoofdwet voor een stoechiometrische, adiabatische verbranding

Voor een tweede hoofdwet-analyse van een adiabatische verbranding, baseert men zich op een exergiebalans. Vermits er geen warmte- en arbeidswisselingen plaatsvinden, wordt deze exergiebalans geschreven als:

met B = H-T_omgS. Hierbij dient opnieuw rekening gehouden te worden met het feit dat het hier over verschillende stofsoorten gaat. Net zoals voor de enthalpie H, zal ook de entropie S uit 2 componenten bestaan een referentieentropie s₀ en de entropie s t.o.v. deze referentie. Deze referentieentropie s₀ kan in principe bepaald worden uit de wet van Nernst (de derde hoofdwet van de thermodynamica die zegt dat alle kristallijne stoffen gelijk zijn aan 0 bij 0K). Deze referentie-entropiewaarden zijn in tabelvorm beschikbaar bij een referentie druk en temperatuur (meestal 1 atm en 25°C).

Voor de stoechiometrische verbranding betekent dit dat

of rekening houdend met (1):

Door de entropiewaarden verder op te splitsen in de twee termen en mits gebruik te maken van

vindt men dat

Om de notatie te vereenvoudigen wordt de volgende notatie ingevoerd b=h-T_omgs die genomen wordt ten opzichte van de referentietoestand.

Dit wil zeggen dat de verbranding kan geïnterpreteerd worden alsof er per kg brandstof een hoeveelheid warmte op oneindig hoge temperatuur wordt toegevoegd. Daarbovenop wordt een zekere hoeveelheid beschikbare arbeid toegevoegd aan het systeem omwille van de hogere entropie die vervat zit in de eindproducten van de chemische reactie.

Tweede hoofdwet-analyse voor een adiabatische verbranding met grote luchtovermaat

Ook voor de tweede hoofdwet-analyse voor een verbrandingsproces met ruime overmaat aan lucht kunnen we een analoge redenering opbouwen. De tweede hoofdwet wordt nu:

Rekening houdend met (1) en (2) om de verbanden te leggen tussen de verschillende stofsoorten, kan deze vergelijking verder uitgewerkt worden.

of voor een zeer grote overmaat aan lucht

De term met de standaard reactie-entropie kan verwaarloosd worden ten opzichte van de term met de verbrandingswaarde. Hierdoor wordt bovenstaande vergelijking vereenvoudigd tot

Dit kan dan voor de eenvoud geïnterpreteerd worden alsof de stromingsexergie die de brandstof invoert in het systeem gelijk is aan de verbrandingswarmte vermenigvuldigd met de omgevingstemperatuur. De chemische energie die in de moleculen beschikbaar was, wordt dan verondersteld om zonder enige irreversibiliteit overgedragen te worden naar het fluïdum, Alsof de verbranding chemische arbeid beschikbaar stelt (of Q op oneindig hoge temperatuur aanlevert).

Bij wijze van voorbeeld vind je hieronder de verbrandingswaarde en de term die gepaard met de standaard-reactieentropie (zie hiervoor de getabelleerde waarden):

Voor C+O₂→CO₂ is Q_p = 393,520 kJ/kmol C, terwijl T_omg∆S₀ = 900 kJ/kmol C

Voor CH₄+2O₂→CO₂ + 2H₂O is Q_p = 890,330 kJ/kmol C, terwijl T_omg∆S₀ = -7035 kJ/kmol CH₄